2.エネルギー技術
2-4 燃料電池
自然エネルギー以外の新エネルギー技術として、なぜか注目されているのが、燃料電池である。燃料電池の仕組みは、大雑把に言って水の電気分解の逆反応によって電気を得るというものである。
しかし、燃料電池の本質は、電力供給というよりは、蓄電装置、それも非常に高価で効率の低い蓄電装置でしかない。その非効率性は、政府機関が導入した本田やトヨタの燃料電池車が極めて高価なものである事からも容易に推測される。
燃料電池の利点として、運用段階における排気ガスが水蒸気であり、『クリーン』であり、発電効率が高いことが挙げられる。しかしこれはまやかしである。まずクリーンというならば、電力供給システムで配電される電気は、運用段階で水さえ出さないのであるから、よりクリーンで扱いやすい。また、燃料電池の発電効率は、『燃料』としての水素に対する効率であって、工業的に燃料電池システムを成り立たせているのは石油による工業生産システムであって、燃料電池システムに投入される石油に対するエネルギー産出比で比較しなければ現実的な評価は得られないのである。
燃料電池は、例えば、宇宙空間であるとか、極めて特殊な環境において、エネルギー効率以外の使用価値がある『かもしれない』が、通常の社会生活のおいて利用する必然性は存在しない。ここでは、燃料電池を一般的な電力供給システムとして運用する場合における、対石油消費におけるエネルギー効率の視点から考えることにする。
2-4-1 燃料電池システムの構成要素
a. 水素製造プラント
燃料電池の『燃料』は水素である。水素は極微量ではあるが大気中に存在する。しかしながら、大気組成における割合は、5×10-5
%程度であり、極めて拡散したエントロピーの高い状態にある。大気中から水素を取得するためには膨大なエネルギー投入が必要であるため実質的に不可能である。
そこで、工業的に水素を製造することが必要になる。水素製造は、水を原料とした電気分解法や、メタノールや炭化水素ガスを原料とした熱化学水素製造法等がある(脱炭化水素燃料を目的とするならば、炭化水素ガスの改質による水素製造は論理矛盾であり、後述するようにバイオマスを使ったメタノール製造は別の深刻な環境問題を引き起こす。)。燃料電池を一般的に運用するためには、巨大な水素製造プラントが必要になる。水素製造プラントの建設に投入されるエネルギーをw11とする。ここでは、電気分解法を前提に議論を進めることにする。水素製造プラントで使用される電力は、勿論最も効率的な火力発電による電力を使用するので、発電におけるエネルギー産出比はα=0.35、投入される石油エネルギーをw12とする。
水の電気分解では、理論的には2個の電子で1水素分子が得られるはずであるが、工業的な生産における水素製造効率をβ=0.7〜0.8程度と仮定する。
水素は軽い気体であり、そのままの利用ではあまりにもエネルギー密度が低く、また体積が大きすぎるため、高圧容器に充填しなければならない。通常200〜300気圧で運用されているようである。この圧縮工程には莫大な仕事が必要であり、充填する水素の持つエネルギーに対する投入仕事の比率は、γ=0.3〜0.4程度と仮定する。
b. 燃料電池
こうして得られた水素を『燃料』として『発電』を行う。現在の燃料電池システムが非常に高価であることから、燃料電池そのものの製造に対して、莫大なエネルギー
w13
の投入が必要であることが推測される。高いといわれる燃料電池の水素燃料に対する発電効率であるが、せいぜいη=0.4〜0.6程度と、それほど高いとは言えない。燃料電池の運用で、電熱併給(コジェネレーション)で効率を稼ぐといっていることからも発電段階の熱エントロピー
gsの発生量は少なくない。ここでは、純粋に発電効率を算定することが目的なので、電熱併給は考慮しない。
c. インフラストラクチャー
更に、家庭・事業所などにおける分散型の電力供給システムとして燃料電池システムを運用するためには、水素ステーションをはじめとする多くの社会的インフラの整備が必要になる。ここに投入されるエネルギーを
w14 とする。
2-4-2 燃料電池システムの『発電』効率
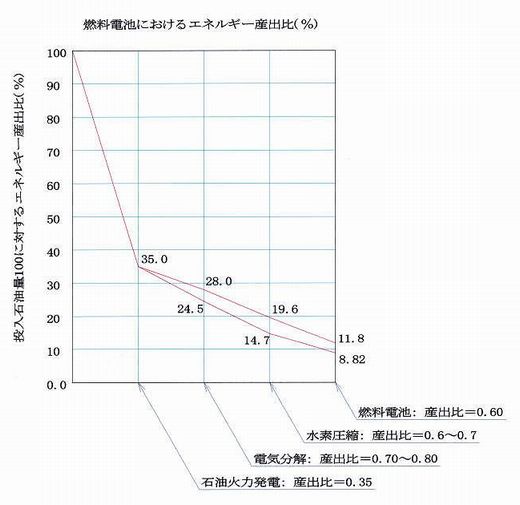
まず、水素製造プラントに投入される電力は次式で与えられる。
αw12
水素製造プラントにおける水素(気体水素に蓄えられる電気エネルギー)の産出は次式で与えられる。
αβw12
製造された水素を高圧容器に充填するために消費される仕事は次式で与えられる。
αβγw12
以上より、燃料電池に投入される水素燃料の持つ電気エネルギーは次式で与えられる。
αβw12 − αβγw12 = αβ(1−γ)w12
燃料電池から出力される電気エネルギーw0は次式で与えられる。
w0
= αβ(1−γ)w12 − Tgs = αβ(1−γ)ηw12
ここに、
α = 0.35
β = 0.7〜0.8
γ = 0.3〜0.4
η = 0.4〜0.6
以上より、
∴ w0 = (0.056〜0.118)w12
ここから、水素製造プラント建設に要する仕事w11、供給電力の生産に投入された仕事w12、燃料電池製造に投入される仕事w13、インフラ整備に投入される仕事w14を差し引くことによって、燃料電池からの実質の電気エネルギーの産出
w は以下の通りである。
w = (0.056〜0.118)w12 − w11 − w12 − w13 − w14
= (−0.882〜−0.944)w12 − w11 − w13 − w14 < 0
エネルギー産出比は、
w0/(w11 + w12 + w13 + w14) << (0.056〜0.118)
2-4-2 燃料電池システムの効率改善の可能性
再び、燃料電池からの産出の式を以下に示す。
w0 = αβ(1−γ)w12 − Tgs = αβ(1−γ)ηw12
さて、燃料電池の発電効率の改善とは、上式における η
の改善である。α、β、γについては、燃料電池に投入される圧縮水素製造プロセスに関する効率であり、大幅な改善はない。今後 η
が如何に改善されようとも、総合的な効率の低さが劇的に改善される可能性は皆無である。燃料電池を『発電装置』として考えた発想そのものが誤りであった。
2-4-3 燃料電池システムの考察
a. 燃料電池システムは高価で低効率な蓄電装置
荒っぽい見方をすれば、燃料電池システムとは、何らかの他の発電システムで産出された電力を、水素イオンに蓄電して、水素を分子レベルの蓄電装置として使うということである。その水素という蓄電装置から蓄電した電力を回収する装置が燃料電池である。
さて、燃料電池は、電力として供給されたエネルギーを何段階もの迂回過程を経て、最終的に再び電気エネルギーとして出力する。供給される(あるいは蓄電する)電力は、前出の表現を使うと、0.35w12であり、これに対して燃料電池からの出力は
w0 =
(0.056〜0.118)w12であり、蓄電量の1/3以下しか回収できない。燃料電池は、蓄電装置としても極めて低効率だと言わねばならない。
b. 燃料電池の使用価値
通常の電力供給システムによって電力を供給できる環境にある住宅や事業所において、わざわざ蓄電装置、それも極めて低効率で高価な蓄電装置を使う必然性はない。
では、燃料電池の使用価値とは何であろうか?考えられる一つの理由は、既に紹介した環境省の『風力発電〜水素製造プラント〜燃料電池システム構想』で示されるように、極めて不安定な自然エネルギー発電システムからの低品質の電力に対する蓄電装置としての利用である。この環境省のアイディアが妥当性を持つためには、第一条件として、自然エネルギー発電など、石油代替エネルギー供給システムが、文字通り石油消費なしにエネルギー供給システムとして成立しなければならない。しかし、既に検討してきたように、石油消費を前提としない限り、これらの『石油代替』エネルギー供給システムは存在できないのである。
自然エネルギー発電の低品質の電力を燃料電池システムに投入可能であるということは、石油消費が行われていることを意味する。それならば、既に見てきたように、石油浪費的な発電システムである自然エネルギー発電システムに石油を投入せず、石油火力発電を用いるのが最も効率的である。石油火力発電による高品位の発電システムには蓄電装置は不要である。故に、分散型エネルギー供給システムとしての燃料電池利用は、全く無意味である。
現在、トヨタ、本田はじめ自動車メーカー各社の行っている、燃料電池という蓄電装置を用いた電気自動車開発も全く同じである。石油が枯渇すれば、石油代替エネルギー供給システムは利用不能であるから、移動用動力源としての燃料電池蓄電システムも全く無駄である。燃料電池車とは、石油文明下の高価なおもちゃに過ぎない。
2-4-3 結論
燃料電池システムは、高価=資源浪費的で、低効率な蓄電装置でしかない。このようなシステムを敢えて使わなければならない必然性のある状況は地球上に存在しない(宇宙空間については知らないが・・・)。
(2004/06/18)
2-5 バイオマス
2-5-1 バイオマス利用の歴史的教訓
バイオマスとは、生物起源の物質の総称である。動植物の体組織、それに動物の糞もバイオマスである。歴史的にみると、工業化以前の主要なエネルギー源は、ほとんど全てバイオマスであったと考えられる。日本の木炭は、非常に優れたバイオマス燃料である。
非常に長い歴史を持つバイオマス燃料であるが、これは既に触れたように主として工業化以前に、炊飯や採光などに用いられていた。
産業革命後、ヨーロッパにおいてバイオマスを工業用燃料として組織的に利用した一時期があった。産業革命後の鉄鋼生産において、木炭は優れた還元剤として、高品質の鋼を得るために大量に利用され、ヨーロッパの広大な森林を食い潰したことは周知の事実である。
環境問題として、現在最も憂慮すべき問題の一つは、生態系の回復速度を超える森林消失であり、あるいは農地の消失である。つまり、バイオマスの再生産性の低下であり、絶対量の減少である。
このような状況下において、エネルギー効率を云々する以前に、石油代替エネルギーとしてバイオマスあるいは、燃料用バイオマスを栽培するために農地を、組織的かつ大量に利用することは、まったく愚かな発想と言うほかない。
2-5-2 炭素循環
地球上の炭素循環の概略を次の図に示す。
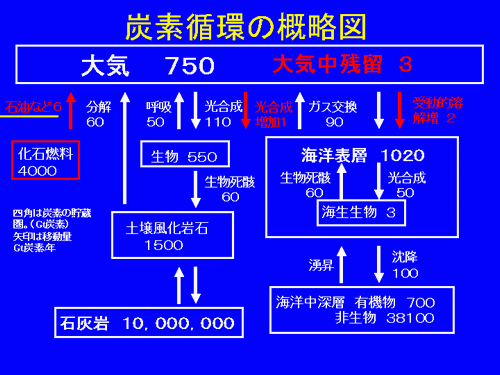
上図に赤色で示されている通り、年間の炭化水素燃料(化石燃料)の燃焼による二酸化炭素に含まれる炭素量は約6Gt(=ギガトン=1,000,000,000トン)程度といわれる。これに対して、バイオマスと考えられる地上生物に含まれる炭素量(ストック)は約550Gt、生物死骸に含まれる炭素量(フロー)は年間約60Gtである。つまり、平均的に炭素量として年間約60Gtの地上生物が新たに生まれ、それに見合うだけ死んでいることになる。
この60Gtの炭素に対応する生体物質=バイオマスのうち、多くは食糧になり、また植物を育てるための土壌を形成することになる。もしここから工業的なエネルギーを得るために、炭素量にしてGtオーダーでバイオマスを利用することになれば、かつての木炭製鉄の例を引くまでもなく、生態系の物質循環は急速に衰えることは明らかである。
生態系の物質循環に基づく定常性を維持しつつ、これを乱さない範囲で行われるバイオマスの燃料としての利用まで否定する必要はないであろうが、莫大な石油消費に支えられた現在のエネルギー供給システムの代替として、組織的かつ大規模な利用は直接的な環境破壊であり、行ってはならない。
バイオマスの燃料としての利用において、バイオマスの燃焼によって発生する二酸化炭素は、再び光合成生物によって固定されるので、大気中二酸化炭素量が増えることはない、という説明がされることがあるが、これは正しくない。
光合成によって生物体に固定された炭素は、一旦地表へ堆積して土壌を形成し、その後徐々に風化作用によって分解されて二酸化炭素として大気へ戻って行く。
バイオマスを燃料として消費することは、生態系の物質循環を衰えさせるばかりでなく、バイオマスの燃焼を起源とする二酸化炭素は、地表に土壌として堆積することなく、速やかに大気中に放出されるため、堆積と風化のバランスを乱す。大気中への二酸化炭素の放出という意味では、石油の燃焼と同じである。
2-5-3 結論
バイオマス利用の基本は、生態系の物質循環を豊かにするものでなくてはならない。バイオマスの燃料としての使用は、生態系の物質循環への適切な還元方法のない廃棄物の処理法として、最小限に止めるべきであり、石油代替を目的とした大規模かつ組織的な使用はしてはならない。
(2004/06/23)
2-6 ヒートポンプ
2-6-1 ヒートポンプの理論 〜企業の宣伝HPから〜
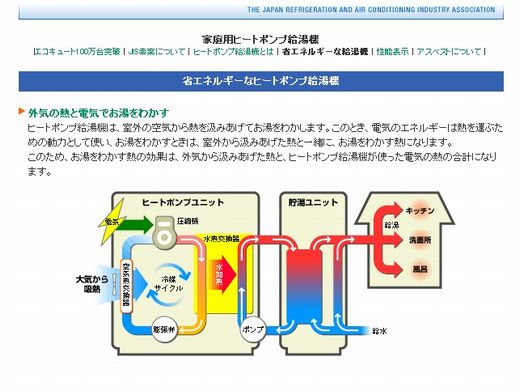
まずはじめに、企業の説明を見ておくことにします。ここでは、社団法人日本冷凍空調工業会のHPの説明の一部を紹介しておきます。
http://www.jraia.or.jp/product/heatpump/saving_01.html
2-6-2 熱エネルギーと力学的エネルギー
御存知のように、初等物理学で習う(今はどうなのでしょうか・・・?)4.2J≒1calという関係が知られています。この関係を用いると熱エネルギーと力学的エネルギーは同じ単位で表すことが出来ます。
しかし熱エネルギーと力学的エネルギーは質的に大きく異なっています。熱エネルギーはS=Q/T(ここに、Qは熱量で単位はJあるいはcal、Tはその温度で単位は絶対温度K、Sはこの熱量の有するエントロピー)というエントロピーを持つエネルギーです。しかし力学的エネルギーはエントロピーを持たないエネルギーです。
その結果、力学的エネルギーは熱エネルギーに100%変換することが可能ですが、熱エネルギーを力学的エネルギーに変換する場合にはエントロピーを除去するために必ず『廃熱』という形で環境に熱を捨てなければならないため100%を力学的エネルギーに変換することは出来ないのです。詳細につきましては後述するとして、ここでは熱エネルギーと力学的エネルギーは質的に異なるという点を理解しておいてください。
エントロピーについて少し触れておくと、エントロピーの大きなエネルギーほど利用価値の少ないエネルギーと理解すればよいでしょう。100℃(=373K)、100calの熱と、0℃(=273K)、100calの熱のエントロピーを比較すると、前者のエントロピーは100/373=0.268cal/K、後者は100/273=0.366cal/Kです。つまり100℃の熱=高温の熱ほど有用なエネルギーということが出来ます。
地球の表面環境では大気温度は平均的に15℃(288K)程度であり、地球大気全体に含まれている熱エネルギーは膨大な量になります。しかし、この大気に含まれる熱エネルギーは温度が低く拡散したエネルギー(=エントロピーの大きい熱エネルギー)なので、利用価値は余りありません。また、熱エネルギーは温度差がなければ力学的なエネルギーとして取り出すことが出来ません。そのため、残念ながら大気に含まれる熱エネルギーを利用することはそれほど簡単なことではないのです。
ヒートポンプとは、大気の持つ常温熱エネルギーを利用するために力学的な力を加えて温度の勾配を作り出す装置です。
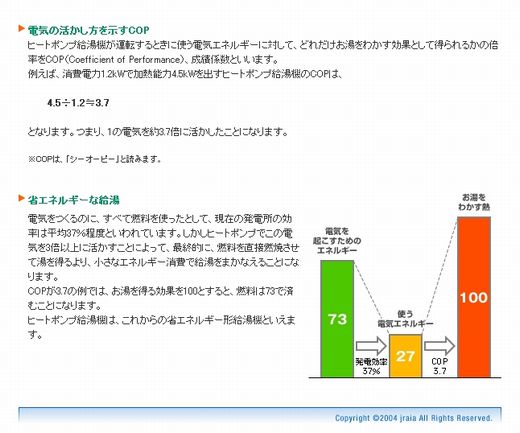
ヒートポンプの説明の中に示されているCOP(Coefficint Of
Performance)という数値に惑わされている方が多い様です。COP>1.0であることを『エネルギーの拡大再生産』=永久機関が可能と勘違いする人も多いようです。
また、説明では『COP=3.7』としていますが、これでは説明不足です。この値は大気温度と供給熱の温度によって大きく変動する数値なのです。
確かに、電気によって熱を供給する場合、通常の電熱器ではCOP<1.0、ヒートポンプは理論上COP>1.0なので、ヒートポンプのほうがすぐれているように見えます。しかし、供給熱の温度が高温になるほどヒートポンプのCOPは小さくなり1.0に近づきます。おそらくある温度を越えれば、装置の複雑さまで考えた総合的なエネルギー利用効率では電熱器のほうが有利になるはずです。それ故、調理用のIHヒーターにヒートポンプ利用の調理器具が取って代わることはないのです。
どのような技術にも適用限界があるものです。ヒートポンプは電気冷蔵庫、エアコンにおいては有効ですが、特段画期的な技術ではなく、あまり大きな期待をすべきではありません。
2-6-3 電動機ヒートポンプ
さて、熱エネルギーの特性が分かったところで話を元に戻します。まず社団法人日本冷凍空調工業会の説明で問題となるところは、ヒートポンプへの入力するエネルギーとして力学的エネルギーから話を始めているところです。これでは現実のエネルギー的な評価は出来ません。工業的な技術を成立させている本質的なエネルギーとは石油あるいは石炭の燃焼熱のエネルギーです。まずここまで遡って議論を始めることにします。
社団法人日本冷凍空調工業会の説明にあるヒートポンプは、電動機から得られる力学的な仕事を利用しています。電動機を動かす電気は火力発電所で作られています。電気を作るまでの素過程の概略を示すと以下の通りです。
燃焼熱↑→熱機関↑→力学的エネルギー↑→発電機↑→電気
※『↑』は環境への熱エネルギーの散逸を示す。『→』は有効なエネルギーの流れを示す。
次に、ヒートポンプで大気から高温熱を取り出すヒートポンプの素過程の概略を次に示します。
電気↑→電動機↑→力学的エネルギー↑→ヒートポンプ↑→熱
この二つの過程を直結することによってヒートポンプの本質的な効率を論じることが可能になります。
2-6-4 温度条件によるCOPの変化 〜ヒートポンプの適用限界〜
さて、ヒートポンプについて熱学的に考えてみることにします。熱学の基本的な条件は、エネルギー保存則とエントロピー増大則です。ヒートポンプについてこの二つの条件を表すと次式になります(槌田『熱学外論』p.111)。
q2 + w = q1
q2/T2 + gs = q1/T1
ここに、
q2,T2 :低温側の熱量及びその温度
q1,T1 :高温側の熱量及びその温度
gs :ヒートポンプのエントロピー発生量
w :ヒートポンプに加える仕事
高温熱を取り出す場合は、上の2式からq2を消去して、
q1 = {T1/(T1−T2)}(w−T2・gs)
となります。ヒートポンプから得られる高温熱エネルギーq1は、ヒートポンプにおけるエントロピー発生をゼロとすると、
q1 = {T1/(T1−T2)}w
となります。社団法人日本冷凍空調工業会のHPの給湯器の定格運転の条件、外気温度(=低温側温度)T2=16℃=289K、給湯温度(=高温側温度)T1=65℃=338Kだとすると、
q1 = {338/(338−289)}w = 6.9w
つまり、ヒートポンプに投入した仕事の6.9倍の熱量が得られることになります。これは、ヒートポンプの理想的な効率であり、COP=6.9に相当します。実際のヒートポンプは、HPのデータではCOP=q1/w=3.7となっていますので、ヒートポンプにおける発生エントロピーは小さくないようです。
発生エントロピーは装置の特性と外気温と供給熱の温度によって変化することになりますが、ここでは、実際のCOPと理想的な場合のCOPの比率を便宜的に発熱効率η=3.7/6.9=0.54に固定して推定することにします。ηを用いると、実際の発熱量は次の式で与えられます。
q1 = {T1/(T1−T2)}(w−T2・gs) ≒ 0.54{T1/(T1−T2)}w
∴COP = q1/w = 0.54{T1/(T1−T2)}
外気温度T2をT2=16℃=289Kに固定すると、
COP = 0.54{T1/(T1−289)}
になります。
ヒートポンプを利用したほうが、燃料の燃焼熱を直接利用するよりも有効である範囲を求めることにします。社団法人日本冷凍空調工業会のHPによりますと、現在の発電の効率は37%ですから、COP=1/0.37=2.7以下であれば燃焼熱を直接用いた方が省エネルギーになるということになります。この温度を求めるとT1=361K=88.3℃になります。
沸騰水を得るためにはヒートポンプを用いるより、燃料の燃焼熱を用いるほうがすぐれているのです。つまり、調理用の器具程度の温度を得ようとすれば、最早ヒートポンプを使用する意味はないのです。勿論、省エネルギーという観点からは、ヒートポンプよりも更に効率の低い電熱器を用いる調理器を使う意味は全くありません。
省エネルギーという観点から電熱器を用いる合理性は全く存在しないのですが、とりあえずここでは熱を得るために電気を使用するという条件下で、ヒートポンプと電熱器による効率の分岐点を推定しておくことにします。
COPが1.0になる温度T1を求めると、T1=628K=355℃になります。通常の電熱器ではCOP<1.0ですが、ここではこれを便宜的にCOP≒1.0だとすると、355℃程度がヒートポンプの使用限界と考えてよいでしょう。実際には通常の電熱器に比べてヒートポンプは装置の機構が複雑になりますから、装置製造に関わるエネルギー投入を含めた総合的な判断としてはそれほど妥当性を欠くものとは考えられません。この特性から、ヒートポンプを調理用の電熱器の代替とする可能性もありません。
以上検討してきたように、ヒートポンプを高温熱を供給する装置とした場合に有効な範囲とは極めて限られていることが分かります。ヒートポンプが有効なのは冷却装置と低温熱の供給、具体的には暖房、給湯(?)程度に限られるのです。給湯に関しては熱湯(沸騰水、100℃)の供給や寒冷地の使用などの条件下では、最早ヒートポンプを利用すべき妥当性は失われますので『?』です。結局、ヒートポンプが確実に有効である電気器具とは、冷蔵庫とエアコン程度しか存在しないのです。それ故この二つの電気製品は早くからヒートポンプを使って製品化されていたのです。
蛇足ですが、給湯器に関しましては、従来の電熱器を用いた電気温水器に比べれば省エネルギーですが、石油やプロパンガス、天然ガスの燃焼熱を直接用いる瞬間湯沸かし器に比べれば明らかに、あるいは普遍的にすぐれているとはいえないのです。
2-6-5 ヒートポンプの効率改善
ここでは、ヒートポンプの効率を改善することを考えます。これまで考えてきたヒートポンプは、圧縮機に対する入力としての仕事を電動機で得ることを前提として考えてきました。その過程をもう一度確認しておきます。
燃焼熱↑→熱機関↑→力学的エネルギー↑→発電機↑→電気↑→
電動機↑→力学的エネルギー↑→ヒートポンプ↑→熱
この図を見て分かるように、電動機ヒートポンプでは、燃料の燃焼熱を熱機関を用いて力学的エネルギーに変換し、発電機を回して一旦電気に変換した後に、また力学的なエネルギーに戻すという無駄なプロセス(水色の着色部分)が含まれています。この各段階で有効なエネルギーの一部が廃熱として捨て去られています。
そこで、この無駄なプロセスを省くとヒートポンプの効率はかなり改善することが出来ます。改善されたヒートポンプの素過程の概略は次の通りです。
燃焼熱↑→熱機関↑→力学的エネルギー↑→ヒートポンプ↑→熱
しかし、家庭で使用するためには熱機関は小型化が難しいので現実的ではないかもしれません。そこで熱機関の代わりに熱化学機関、例えばガソリン・エンジンやディーゼル・エンジンで置き換えてやるのが現実的です。
熱化学機関↑→力学的エネルギー↑→ヒートポンプ↑→熱
発動機(ここでは熱化学機関)からの廃熱は、力学的なエネルギーを得るには低温すぎるのですが、水を加熱する給湯器の熱源として用いるには十分な温度を持っています。発動機ヒートポンプでは、発動機の冷却を水冷にしてやれば、これを給湯器の熱源として回収出来るという利点があり、システムに投入された燃料に対する熱効率は飛躍的に改善されることになります。
迂回度を減らすことによってシステムの効率は改善されるのです。したがって、電気を使わなくてすむことは電気を使わずに行うほうが圧倒的に効率が良くなるのです。つまり逆に考えれば電力化は一般的にエネルギー利用効率を落とすのです。
2-6-6 熱エネルギーの『質』を考える
熱エネルギーはエントロピーを持つエネルギーであり、エントロピーの大きな熱=低温の熱ほど利用価値が小さいことを既に述べました。ここでは熱を力学的なエネルギーに変換する熱機関の効率について考えてみることにします。
熱機関、ここでは水蒸気タービンの熱効率を考えます。水蒸気タービンとは、作動物質として水を利用する熱機関です。通常の火力発電で用いられる水蒸気タービンでは、500〜600℃、200〜300気圧程度の高温高圧水蒸気を利用し、100℃程度で廃熱します。
熱機関のエネルギー収支とエントロピー収支は次の式で与えられます。
Q1 = Q2 + w
Q1/T1 + gs = Q2/T2
ここに、
Q1,T1 :高温熱源の熱量及びその温度
Q2,T2 :廃熱の熱量及びその温度
gs :熱機関のエントロピー発生量
w :熱機関から得られる仕事
この2式から熱機関から得られる仕事量を求めると次のようになります。
w = Q1{(T1−T2)/T1}−T・gs
上式の右辺の第一項は、熱機関で得られる理想的な仕事量(力学的エネルギー)を示し、熱機関に投入された熱量Q1の係数η0={(T1−T2)/T1}=(1−T2/T1)は理想状態の熱効率です。これはカルノー・サイクルの熱効率として知られていますが、現実にはこの過程を実現するため(発生エントロピーgs=0にすること)には無限大の時間を要することになり実現不可能です。熱機関の効率改善とは、発生エントロピーを出来るだけ小さくすることです。
火力発電の高温水蒸気温度をT1=600℃(=873K)、廃熱温度をT2=100℃(=373K)として理想状態の熱効率を求めると、
η0=(1−T2/T1)=(1−373/873)≒0.57
になります。実際の火力発電では、熱効率はη1=0.4
程度です。実際の熱効率と理想的な熱効率の比を求めるとη=η1/η0=0.4/0.57≒0.7になります。便宜的にこの数値は一定としておくことにします。このとき、熱機関から得られる仕事量は次の式で求めることが出来ます。
w = Q1(1−T2/T1)−T2・gs≒η・Q1(1−T2/T1)=0.7Q1(1−T2/T1)
上式から分かるように、熱機関で得られる仕事量は、熱機関に加えられる高温熱源の温度と廃熱の温度によって決まり、温度差が大きいほど熱効率が高くなります。作動物質が水である蒸気タービンでは廃熱の温度は100℃程度ですから、熱効率を上げるためには高温熱源の温度をいかに高くするかが問題になります。
例えば、高温熱源の温度を200℃(=473K)まで下げると、得られる仕事量は
w =0.7Q1(1−T2/T1)=0.7Q1(1−373/473)=0.15Q1
にまで減少します。これが『低温の熱ほど利用価値が低い』という意味なのです。
2-6-7 第二種永久機関は可能か?
ヒートポンプを用いることによって投入仕事wを得るために投入する電力量(≒w)に対して、q1=COP・wの熱量を得ることが出来ます。q1=COP・wがヒートポンプに投入された電力量wを得るために必要な熱量Q1よりも大きければ、電力の拡大再生産が可能ではないか?
この疑問点で見落とされていた視点は、熱の温度の問題です。言い換えれば熱エネルギーの持つエントロピー量による『質』についての視点が欠落していたのです。
現状の熱効率の電動機ヒートポンプでは、得られる高温熱の温度T1が88.3℃以上になれば、発電に投入された燃料の燃焼熱を直接用いたほうが効率が良いことを示しました。88.3℃では水を沸騰させることが出来ませんからそもそも水蒸気タービンは成り立たないのです。
では、電動機ヒートポンプから通常の火力発電と同程度のT1=600℃の高品質の熱エネルギーを得る場合のCOPを求めてみると以下の通りです。
COP = 0.54{T1/(T1−289)}=0.54{873/(873−289)}=0.8
社団法人日本冷凍空調工業会のHPで示された発電効率0.37を用いると、電動機ヒートポンプから得られた高温熱で得られる電力量は、
w'=0.8w・0.37=0.296w≪w
となり、永久機関どころか1/3以下にまで減少してしまうのです。
例えば、熱機関として作動物質として水以外を用いることも考えられますので、高温側温度をT1、低温度側温度をT2とした一般的な議論をしておきます。前回示したヒートポンプの給熱量と今回示した熱機関の仕事量の式
q1=0.54{T1/(T1−T2)}w 電動機ヒートポンプからの熱量
w=0.7Q1{(T1−T2)/T1} 熱機関を用いた発電電力量
から、q1=0.378Q1となり、電動機ヒートポンプから得られる熱で投入した仕事を再生産することは出来ないことが分かります。
現状では、まったくお話にならないのですが、それでも発電効率や電動機ヒートポンプの改良で、発生エントロピーを極限まで減らした場合はどうなるのでしょうか?これは両システムの発生エントロピーをgs→0とした場合の極限として表すことが出来ます。この時の熱機関を用いた発電装置の発電量はw
= Q1{(T1−T2)/T1}、ヒートポンプの供給熱量はq1 = {T1/(T1−T2)}wになります。この場合、次の等式が成り立ちます。
Q1=q1
つまり、発生エントロピーをゼロとした極限状態において初めて単純再生産になるのです。一般的には、Q1>q1であって、電動機ヒートポンプでは、投入熱エネルギーQ1に対して、供給熱エネルギーq1の方が大きくなることはないのです。永久機関は存在しないし、したがって電力を拡大再生産することは有り得ないのです。
2-6-8 ヒートポンプの実像
以上の検討から、ヒートポンプは冷却ないし比較的低温の熱を供給する場合において有効な技術であり、それ以上ではないことが分かりました。
具体的に利用の妥当性のある電気器具は冷蔵(冷凍)庫とエアコン(冷暖房機)だけであり、これは当初からヒートポンプを利用している技術です。
給湯器に関しては、電熱器を用いる従来の給湯器に比べれば確かにエネルギー節約的ですが、灯油やLPガス、天然ガスを用いる瞬間湯沸かし器タイプの給湯器に比べると明確な優位性は存在しません。
特に、ヒートポンプを利用する場合、瞬間湯沸し器タイプの給湯器は作れないでしょうから、タンクに溜めた温水からの環境への放熱を補うために常時運転が必要になり、しかも装置構造が複雑であることも含めて、おそらく灯油やLPガス、天然ガスを用いる瞬間湯沸かし器タイプの給湯器の方がすぐれていると考えられます。
更に、電動機ヒートポンプはあまりにも迂回度の高い技術であり、条件が許すならば熱化学機関を用いた発動機ヒートポンプを用いる方がはるかに効果的であることを付言しておきます。家庭で利用するには振動音、排気ガスなどの処理の問題などが考えられますが、事業所などでは可能な技術であろうと考えられます。
最後にもう一度確認しておきます。電気を使用しなくても実現できることは電気を使わないことが最も省エネルギー的なのです。電力化はエネルギー資源と鉱物資源の利用効率を低下させます。COPなどというイカガワシイ数値に惑わされないでください。
(2008/01/15)
§3. 結論
3-1 石油文明・工業生産システム
石油文明とは、文字通り石油(石炭、天然ガスなどの炭化水素燃料も含む)によるエネルギー供給システムの能力による工業生産によって成り立っている。
通常、工業生産技術とエネルギー供給システムは分離して考えられている。その結果としてエネルギー供給システムとしての石油の枯渇、ないし最近では二酸化炭素地球温暖化の原因とされる石油の使用に替わって、別のエネルギー供給システムによって工業生産システムを運用しようという発想が生まれた。
しかし、工業生産システムの本質とは、あくまでも石油によって供給されるエネルギーによって運用することを前提に成り立っている、究極的には石油の利用技術の総体なのである。これを石油なしに運用することは論理矛盾であり、不可能である。
3-2 鉱業と工業
これまで見てきたように、石油代替エネルギーと呼ばれる全ての技術は、石油によるエネルギー供給システムなしで自己再生産することが不可能である(対石油エネルギー産出比<1あるいはエネルギー収支<0)。それどころか、発電システムとして石油火力に対して石油節約的ですらない。石油文明下の技術としても、石油利用効率において既存の石油火力発電に劣る事は勿論、その他の鉱物資源を大量に浪費する技術なのである。
石油がエネルギー資源として優れている理由の一つは、それが本質的には地下資源であり、石油が潜在的に有する優れた物性的な性質を獲得するために、何ら工業的なエネルギー投入が必要ない点である(より使いやすくするための精製工程は必要であるが)。我々は、ただその石油を採掘して運んでくることによって、その優れた資源の能力を利用することが出来るのである。石油は鉱業の産物なのである。
これに対して、現在提案されている石油代替エネルギー技術は、全て工業の産物である。既に述べたように、あらゆる工業生産過程は石油エネルギーの消費によって成り立っている。つまり、石油エネルギーを消費して、産出されるものもエネルギーなのである。工業生産過程の生産効率は100%にはなり得ないのであるから、工業生産過程に投入されたエネルギー量に対して産出されたエネルギー量がこれを上回る可能性はほとんどないといってよい(例えば、火力発電や燃料電池システムにおける電気分解による水素製造)。また、エネルギーを得るまでの工業的な工程が複雑かつ多段階になるほどエネルギー損失は大きくなる。
もし、仮に産出エネルギー量が投入エネルギー量を上回ることがあるのならば、それはエネルギーの原料資源の優れた潜在的な能力によるものである(例えば精製された石油燃料)。
これに対して、自然エネルギーの利用は、石油と同じように、もともと自然エネルギーの持つ潜在能力を利用するシステムであるから、投入石油エネルギーに対してエネルギー産出が上回る可能性はある。しかし、既に検討してきたように、自然エネルギーはエネルギー密度があまりにも低く、あるいは時間的な不安定性を制御できないという困難さのため、これを工業技術によって捕捉し、安定運用するためには莫大な石油と鉱物資源の投入が必要となり、現実的には石油火力発電の石油利用効率を上回る可能性はない。
工業生産システムを運用するためには、エネルギー産出比の高いエネルギー(鉱物)資源が必須であり、採取可能な炭化水素系の資源の枯渇によって、今日的な工業生産システムは終息する。全ての『石油代替』エネルギーシステムは、名前とは裏腹に、石油によるエネルギー供給システムの効率の悪いサブ・システムにすぎず、石油の枯渇とともに消滅する。石油文明下における石油代替エネルギー供給技術は、石油と資源の浪費であり、無意味である。
(2004/06/26)
【補足】
今回の連載の途中で、何人かの閲覧者の方から疑問や意見を頂いた。幾つかについて簡単に触れておく。
Q1 石油代替エネルギーシステム運用に投入されるエネルギーを石油としているのはおかしいのではないか?
A1 既に述べてきたように、現在提案されている石油代替エネルギー供給システムの対石油消費のエネルギー産出比は1よりも小さい。これは、このシステムがエネルギーを消費していることを意味し、正味のエネルギー産出量はマイナスである。故に、石油代替エネルギー供給システムのエネルギー『産出』を他のいかなるプロセスに投入することも不可能である。
Q2 揚水発電による蓄電システムを利用した場合の太陽光発電の発電単価はどの程度になるか。
A2 水力発電の発電単価は、14円/kWh
程度とされている。揚水発電では、上下二つのダムが必要であり、更に揚水用のポンプ施設などの付帯設備が必要なので、少なくとも倍程度の発電単価になるであろう。ここでは、25円/kWh
と仮定する。太陽光発電によって供給される電力による揚水効率を70%と仮定すると、揚水発電で1kWh
を発電するために必要な水を汲み上げるために必要な電力量は、1/0.7=1.43(kWh)となり、その価格は
70×1.43=100.1円となる。合計すると、太陽光発電〜揚水発電システムによる供給電力の単価は、少なくとも 125円/kWh
程度であろう。
Q3 燃料電池の使用する水素製造において、光触媒を使った光化学反応による水素製造が実用化すれば、燃料電池システムの利用の可能性があるのではないか?
A3 これは、電力供給において太陽電池を用いるのと基本的に同じ発想である。単に水を日向に置いておくだけでは水素が発生することはない。太陽光の持つエネルギーを利用して光化学反応で水の分解を行う装置が必要になる。太陽光の持つエネルギーを利用する点で、既に失敗している太陽熱発電や太陽光発電と同様に、太陽光エネルギーが工業的な利用を前提にする限り、あまりにもエネルギー密度が低いという問題を克服することは出来ない。既にこの段階で成功はおぼつかないと考えるべきであろう。
太陽光発電では太陽光の電気への変換効率は理想状態で20%程度であるが、果たして光触媒を用いた光化学反応でどれほどの太陽光エネルギーが有効に利用されるであろうか?仮に40%の効率を達成したとしても、実際の野外での運用において、光触媒を用いた土地集約的な水素製造プラントの面積は広大なものになる。
更に燃料電池システムの運用のためには水素の圧縮工程が必要になり、そこで膨大なエネルギー損失を生む。更に、燃料電池システムそのものが高価であることからも分かるように、燃料電池の製造に莫大なエネルギーと希少資源を含む鉱物資源の投入が必要になる。総合的な効率が太陽光発電を上回るのは困難だと考える。石油の代替になる可能性はない。