解題「温暖化の虚像」②

大気中CO2濃度上昇の主因は自然現象①

　地球の表面環境（固体地球の表面付近と海洋と対流圏の大気を指すものとします）の中ではCO2は絶えず循環しています。その概要をIPCC2007年の報告書に掲載された炭素循環図で見ておきます。

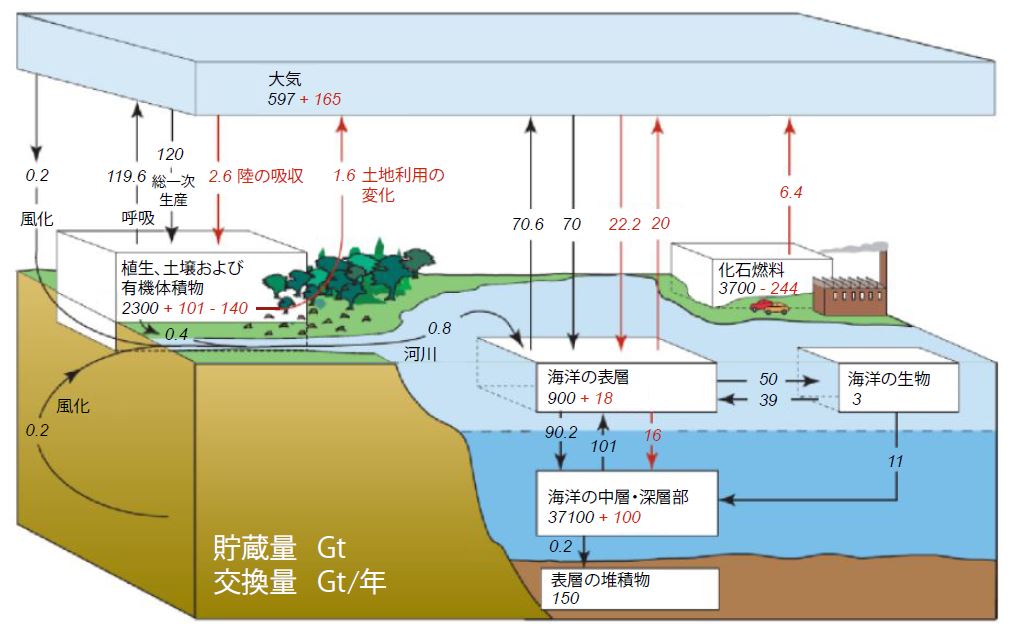
　炭素循環図の黒の数字と矢印は産業革命前の「定常状態」の値を示し、赤の数字と矢印は産業革命以降現在までの増加量を示しています。
　海洋は炭素ないしCO2の巨大なバッファーです。CO2の水への溶解反応は可逆反応であり、化学平衡状態では環境の温度によって大気中のCO2濃度と水の溶存CO2の濃度は一意的に決まります。大気と海洋・地表面との間の炭素循環は海洋の持つ調整能力によって平均的に見ると、常に
　海洋・地表面からのCO2放出量（Gt/年）≒海洋・地表面のCO2吸収量（Gt/年）
の関係が成り立つと考えられます。
　この点について「温暖化の虚像」2－3節「地球の炭素循環」(p.26)において「CO2放出量とCO2吸収量はほぼ均衡している」と書いた点について、以下その理由について考察することにします。

人為的CO2蓄積モデル
　IPCCの炭素循環図の現在における炭素循環では、概要であるにもかかわらず敢えて、海洋・地表面からのCO2放出量が218.2(Gt/年)であるのに対して、CO2吸収量が215.0（Gt/年）であるとしています。不平衡量は3.2(Gt/年)です（→温暖化の虚像p.26）。
　これは、C.D.Keelingが彼の南極とハワイにおける大気中CO2濃度の連続精密観測記録について、「観測期間中の大気中CO2濃度の上昇量は、同期間に化石燃料の燃焼などによって人為的に放出されたCO2の半量程度に相当する」と報告したことを受けて、人為的なCO2放出量6.4(Gt/年)の半量である3.2(Gt/年)が大気中に蓄積していることを示したかったのであろうと考えられます。
　人為的CO2蓄積モデルでは、「海洋・地表面からのCO2放出量が218.2(Gt/年)、CO2吸収量が215.0（Gt/年）」として、その差⊿q=3.2(Gt/年)が毎年積み重なって大気中CO2濃度が上昇していると解釈しています。しかし「CO2放出量218.2(Gt/年)≠CO2吸収量215.0（Gt/年）」という状態が継続的に維持される状態は自然現象として考えられない状態です。

定常開放系
　ある系が物質ないしエネルギーの入出力があり、しかもある一定の状態が保たれているような系を定常開放系と呼びます。太陽光からエネルギーを受け取り、赤外線で放熱している地球も定常開放系です。

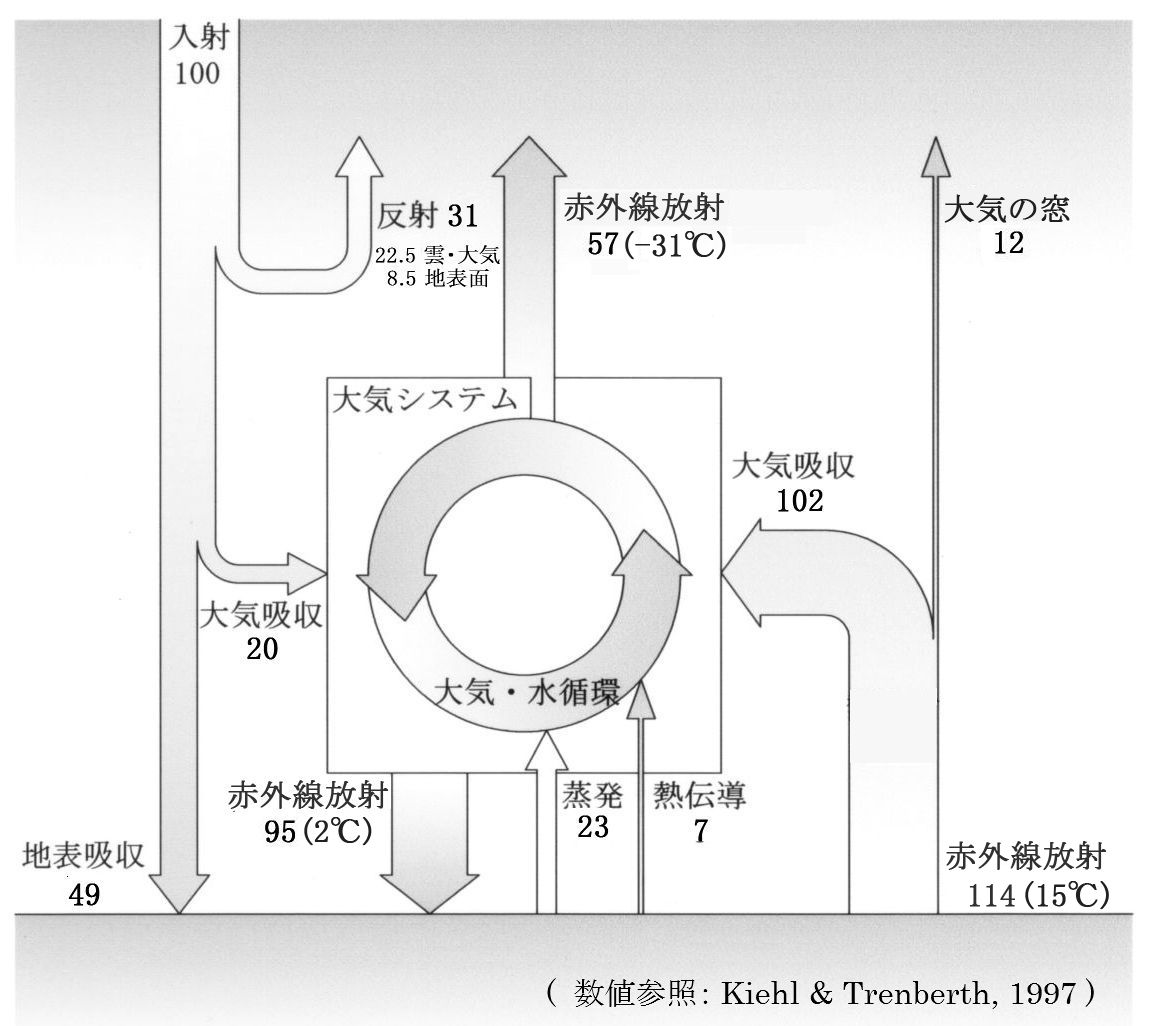
　定常開放系の成立する条件は「入力＝出力」であることです。地球の表面環境の温度状態は「有効太陽放射＝地球からの赤外線放射」を満足するように決まります。
　高校地学の学習指導要領では、
「地球全体の熱収支」については、太陽放射の受光量と地球放射の放熱量が釣り合っていること・・・
を教えるように求めています。
　定常開放系はいたるところに見ることができます。生きている生物は全て定常開放系とみることができます。生物が一定の状態を維持する機構をホメオスタシス、恒常性といいます。
　物質やエネルギーの入出力がありながら、一定の安定した状態を維持している系は、偶然に微妙なバランスが保たれているわけではありません。自然現象は不断に様々な擾乱を受けているにもかかわらず、安定した状態を保っています。それは、そのシステム自身の中に入力と出力を調整する仕組みを持っているからです。

定常性はどのように回復されるのか
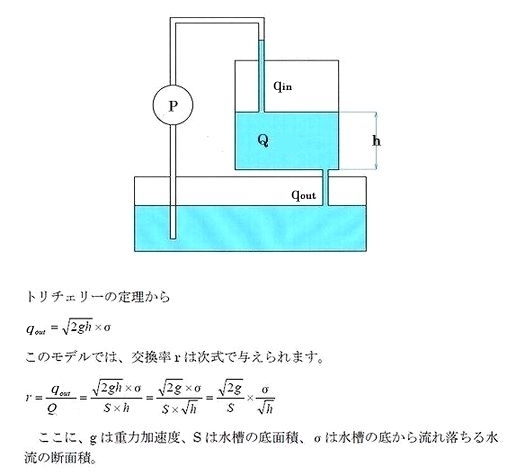
　では定常状態にある系に対して擾乱を与えた場合に、どのように定常性が回復されるのかを簡単な例で考えてみることにします。例として穴の開いた水槽を考えることにします。

• 

　このモデルでは、ポンプで汲み上げられて水槽に注がれる単位時間あたりの水量をq_in、水槽の底の穴から流れ出る水量をq_outとします。水槽にたまっている水の量はQ(=S×h)です。定常状態では、q_in = q_outが成り立ちます。
　ここに擾乱として流入する水量をステップ関数的に⊿qだけ増加させます。この初期状態について上添字「0」を付けることにすると、
q_in⁰+⊿q > q_out⁰
になるため、水槽の水位hが上昇し始めます。水槽の水位hが上昇するにつれてq_outも増加するため、やがて
q_in⁰+⊿q = q_in¹ = q_out¹
となって再び定常状態を回復します。上添字「1」は新しい定常状態を示します。初期の水位をh₀、新たな定常状態の水位をh₁とすると、水位変化の過程を模式的に示すと次のようになります。

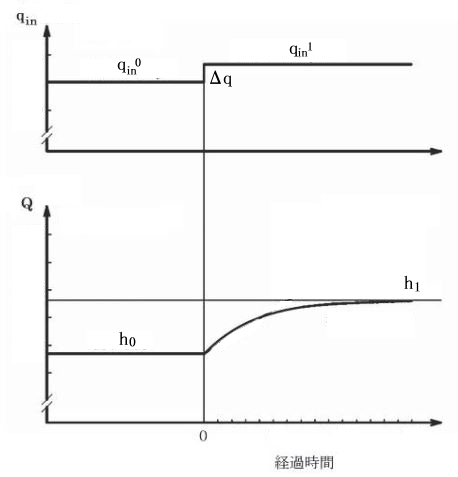
　図に示すように、水槽の水位は新たな定常状態h₁に急速に漸近する上に凸な曲線で表すことができます。これは、q_inとq_outとの差が大きいほど、hの変化速度が大きいことを示しています。
　この例では、q_inをステップ関数的に変化させたため、q_outの応答には有限の時間がかかっています。しかし、q_inを連続的に十分緩やかに変化させるとq_inとq_outは同期して変化するように観測されます。
　この水槽の例で考えると、ポンプの出力を連続的にゆっくり上昇させると、それに伴って水位が上昇し、ポンプ出力の変化を止めると同時に水位の上昇も止まることになります。この間、常にq_in ≒ q_outが成り立っています。
　このように、定常系に対する入力の連続的な緩やかな変化に対して、出力は常に同期して変化するのです。この水槽モデルの具体的な調整機構は、水槽の底から流れ出る水量q_outが水深hの平方根に比例して大きくなるという性質です。
　水位の上昇は単純に「q_inとq_out差が蓄積」されるのではなく、入力と出力と貯水槽を巡る流量の変化によって全体のバランスが変化した結果なのです。

　大気中のCO2量QないしCO2濃度（大気中CO2濃度は0.04％と小さいため、Qと大気中CO2濃度は比例すると考えてよい）は、海洋・地表面からのCO2放出という入力と、海洋・地表面のCO2吸収という出力のバランスで決まります。大気システムは定常系と考えられます。大気中のCO2濃度の変動は十分緩やかです。大気中のCO2濃度が変化していても、常に「海洋・地表面からのCO2放出量q_in（Gt/年）≒海洋・地表面のCO2吸収量q_out（Gt/年）」という関係が成り立っています。
　人為的CO2蓄積モデルでは、入力と出力の差を固定して、その差が毎年蓄積して大気中のCO2濃度が上昇すると説明します。しかし実際の大気では大気中のCO2濃度の上昇に伴って、大気中にあるCO2の海洋への溶解速度q_outが大きくなるため、有限の差が固定されるという現象は起こり得ないのです。

　人為的CO2蓄積モデルについて、日本の人為的CO2温暖化論者のまとめた「権威ある」冊子である東大IR3S/TIGS叢書No.1「地球温暖化懐疑論批判」から彼らの考えを紹介します。
※彼らの用いている記号Qは人為的なCO2 放出量であることに注意。Q = 6.4Gt/年。rは、Qに対する海洋・地表面の吸収率を示す。彼らによるとr = 0.5。

　このように、彼らは人為的なCO2放出がある限り永続的に年間Q×( 1 – r )の割合で大気中のCO2濃度が単調に増加し続けるのが正しい（通常！）、と主張しています（吸収率r = 0.5、つまりQ×(1 – r) は人為的な放出量の半分が大気中に蓄積することを意味する。）。
　これは、定常系の調整機能を全く無視した暴論です。大気中のCO2濃度が上昇すればq_outが増加するため、単調に大気中のCO2濃度が上昇し続けることは自然現象としてあり得ません。「人為的CO2蓄積モデル」は、大気中CO2濃度に与える人為的な影響を大きく見せるために創られた、あまりにも自然現象として不自然かつ異常なモデルと言うしかありません。
　また、海洋・地表面環境から放出されるCO2量は炭素重量で218.2Gt/年であり、人為的な放出はわずか6.4Gt/年であり、3％程度に過ぎません。放出された残りの97％のCO2の行方を無視して、人為的な放出の半分だけが大気中CO2濃度を決定するなどという主張は、余りにも不完全というしかないでしょう。