HP�Ǘ��҂���
No.1247 (2018/12/16) �N���s���ƂȂ����N���̉��g���ɂ�鋺��
�l�דI���g���ŋC����4���㏸���ē��{�̍��l�����ł���H�I
�@���A�C��ϓ��Ɋւ���g�g����24�����c��COP24���J�Â���Ă������߂��A���̂Ƃ��뉷�g���̋��Ђ𐁒�������ڂɂ��܂��BCOP��12���ɍs���邽�߂��A�N���Ƃ����Ή��g���̋��Ђ������s����Ƃ����̂��A���ΔN���s��(��)�ƂȂ����悤�ł��B
�@12����NHK�̃j���[�X�ԑg�ŁA�l�דI���g�������̂܂ܑ�����4���㏸����ƁA���{�̍��l�������ȏ�p�������Ă��܂��ƕ��Ă��܂����BNHK�j���[�X�E�F�u�̋L�����Љ�܂��B
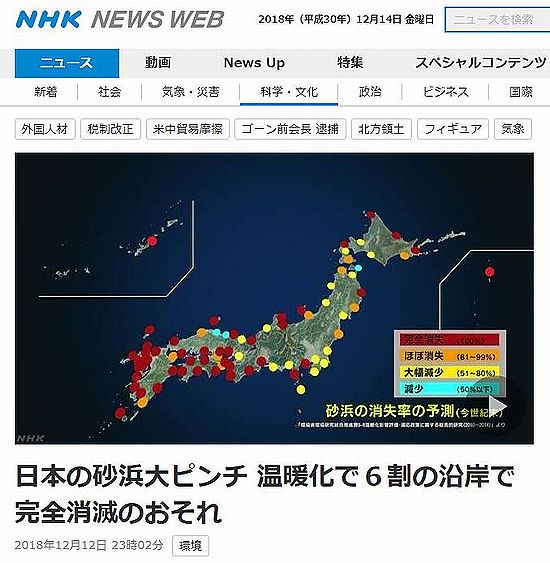
�@�C������T�[�t�B���ȂǂŎ������ɐg�߂ȍ��l����@�ɂЂĂ��܂��B�n�����g���ɂ��C�ʏ㏸�̉e���ŁA�ň��̏ꍇ�A�����I���܂łɓ��{�̂X���̉��݂ō��l�̖ʐς������ȏ㌸��ق��A�U�������S�ɏ����邨����̂��邱�Ƃ����̌����@�ւȂǂ̕��͂ŕ�����܂����B
�@����́A���A�̂h�o�b�b���u�C��ϓ��Ɋւ��鐭�{�ԃp�l���v���S�N�O�̕���26�N�Ɍ��\�������̃f�[�^�Ȃǂ���ɁA���������������w�Ȃ�28�̋@�ւō�錤���O���[�v�������������̂ł��B
�@����ɂ��܂��ƁA����A���E�̕��ϋC������S�x�オ���ƁA���{�̉��݂ł́A�����I���܂ł��C�ʂ��ő��60�Z���`�㏸���A����ɔ����āA�ň��̏ꍇ�A�S��77�̉��݂̂����A96���ɓ�����74�̉��݂ō��l�̖ʐς��A����蔼���ȏ㌸��\���̂��邱�Ƃ�������܂����B
�@����ɁA60���ɓ�����46�̉��݂ł́A���l�̏�������100���ɒB���A���S�ɏ����邨���ꂪ�����Ƃ������Ƃł��B
�@���y��ʏȂɂ��܂��ƁA�S���e�n�̍��l�ł́A���̊J����䕗�ɂ�鍂�g�Ȃǂ̉e���ł��łɏ����⌸�����N���Ă��܂��B
�@���̂����A�_�ސ쌧�̏Ó�C�݂ł́A�Ⴆ�Ί�����s�ŕ���17�N�܂ł�50�N�]��̊ԂɁA�C�ݐ��������ɍő��50���[�g������ނ����ق��A��{���ł́A���Č��̊C������Ɏw�肳�ꂽ��30���[�g���̍��l������A���N�A�C�����ő����̐l���K��}���\�������J�Â���Ă��܂������A11�N�O�̕���19�N�ȍ~�́A��������ł��Ȃ��Ȃ��Ă��܂��B
�@���������n��ł́A�����Ăё��₷�H�����s���Ă��܂����A���g���ɂ�鏫���̌��������������������͂܂��i�߂��Ă��܂���B
�@���̂��ߐ��Ƃ���́A�C�����Ȃǂ̊ό��ʂɉ����A�h�Ђ�Ԍn�̈ێ��ȂǍ��l���ʂ����Ă���d�v�Ȗ�����F�����A����������ׂ����Ƃ����ӌ����o�Ă��܂��B
�ň��V�i���I����������Ɓc
�@�������������Ȃǂ��s�������͂ł́A�����̋C���̏㏸�̓x�����Ȃǂɉ����āA�����̃V�i���I���쐬���A�����̍��l�̏��������v�Z���Ă��܂��B
�@�m�g�j�́A���̂����ň��ƂȂ�V�i���I�ɂ��āA�u�m�l�`�o�r�i�G�k�}�b�v�X�j�v�ƌĂ��V�X�e���ʼn������܂����B
�@�����ɂ������ẮA��������100���ɂȂ鉈�݂́u���S�ɏ����v�A81������99���́u�قڏ����v�A51������80���́u�啝�Ɍ����v�A50���ȉ����u�����v�ƕ��ނ��܂����B
�@���̌��ʁA���͂̑ΏۂƂȂ����S��77�̉��݂̂����A96���ɂ�����74�̉��݂��u���S�ɏ����v��u�قڏ����v�A����Ɂu�啝�Ɍ����v�ƂȂ�A�u�����v�ɂƂǂ܂�̂͂킸���R�ł����B
�@���̂����A���l���u���S�ɏ�������v�Ɨ\�z����鉈�݂́A�u�k���v��u�����v�A�u�O���k�v�Ȃǂ̖k���{�̂ق��A�Ó�C�݂��܂ށu���͓�v�Ⓦ���́u���}���v�A�u�ɓ������v��u�O�͘p�E�ɐ��p�v�Ȃǂ̓��C�n���A�u�\�o�����v��u�ዷ�p�v�Ȃǂ̖k���A�u�I�B��v��u�W�H�v�Ȃǂ̋ߋE�n���A�u�L���v��u���R�v�A�u�y���p�v�Ȃǂ̒����E�l���n���A�u����C�v��u������v�A�u�L���C�v�A����Ɂu���������v�Ȃǂ̋�B�E����ƁA�e�n�ɕ��z���Ă��āA�L���͈͂ō��l����@�ɂЂĂ���̂�������܂��B
���l�����Ŏ��ۂ̔�Q��
���l�̏����⌸���̉e���ō��g�������A�����Ȃǂɔ�Q���o���n�悪����܂��B
�@���̂����A���͘p�ɖʂ���_�ސ쌧���c���s�́u�O��C�݁v�ł́A���l�̌����������Ă��āA�_�ސ쌧�ɂ��܂��ƁA����19�N�܂ł�60�N�ԂɊC�ݐ�����30���[�g�������Ɍ�ނ����Ƃ������Ƃł��B
�@���́A���l�̉�ڎw���A�V�N�O�̕���23�N����C�݂ɍ����^�ѓ����H���𑱂��Ă��܂��B
�@���̍��l�̌����Ȃǂ̉e���ŁA���N10��23���A�C�݂̂����߂��ɂ���s�̎{�݁A�u�O�H�����فv�����g�ɂ���Q���܂����B
�@�����ق́A�C��8.1���[�g���̏��ɂ���܂����A���̓��́A�_�ސ쌧�ɐڋ߂����䕗21���ɂ�鍂�g����h���z���ĉ����A�P�K�ɂ��鑋�K���X���S������A��c�����Z�������Q���o�܂����B
�@�����ق̋߂��ɏZ�ޒŖ���͂���i82�j�́A�������������Ă����Ƃ��ɁA��h���z�����g�̏ォ�炩�Ԃ�A�S�g�����Ԃʂ�ɂȂ����Ƃ������Ƃł��B���̌�A�����ق̊��ꂽ�K���X�̓P����ƂȂǂ��s�����Ƃ������Ƃł��B
�@�Ŗ삳��́u�����Ȃ蓪����g�����Ԃ�Ƃ������Ƃ͍��܂łȂ������̂ŕ|�������B�͍̂��l�������̂��A���͂قƂ�ǂ������ɂȂ��Ă��āA�g�ł��ۂ������ԋ߂��Ȃ��Ă���悤�Ɋ�����B�����̉Ƃ܂ł͂܂��g�͗������Ƃ͂Ȃ����A���ꂩ��C��ϓ��łǂ��ς�邩������Ȃ��̂ŁA��X�����Ȃ���l���Ȃ��Ƃ����Ȃ��Ǝv���v�Ƙb���Ă��܂����B
�@���y��ʏȂɂ��܂��ƁA���̂ق����l���������Ă���e���ŁA����19�N�Ƌ��N�̑䕗�ɂ�鍂�g�ŁA�_�ސ쌧��{���Ƒ�钬�̊C�݉�����ʂ鎩���Ԑ�p���H�A�u���Ão�C�p�X�v�̌�݂����ꂽ��A���ꂽ�肷���Q���o�Ă��܂��B
�@���̂����A���N�̑䕗21���ł́A�o�C�p�X�̌�݂���K�͂ɑ���������H�ʂ��Z�������肵���e���ŁA�S�Ԑ����铹�H�̂����A�C���̂P�Ԑ��������ʍs�~�߂ɂȂ��Ă��܂��B
���l�����̉e�����������Ă݂�
�@���l�̏����⌸�����i�ނ��ƂŁA���g���Z��n�ɂǂ̂悤�ȉe����^����̂��B���Ƃ̋��͂Ŏ������܂����B
�@���g�Ȃǂ̃��J�j�Y���ɏڂ����A������w���H�w���̗L�쑾�Y�����̌����O���[�v�́A����15���[�g���A����50�Z���`�̐������g���Ď������s���܂����B
�@�����ɊC�݂ɂ�����̂Ɠ��������g���č��l�����A���̉��ɒ�h�ƏZ��Ɍ����Ă��͌^��ݒu���܂��B�����ɁA����ȑ��u�Ől�H�I�ɍ��g�����A�������݂܂��B
�@�����̌��ʁA���l������ꍇ�́A���g�͉����ōӂ��č��l���h�͏��z���܂���ł������A���l���Ȃ��ꍇ�́A���g�͒�h�����z���A�Z��ɑł����܂����B
�@�L�싳���ɂ��܂��ƁA���l�̏����⌸�����i�ނƁA���ꂾ���C�ݐ��ƏZ��n���߂��Ȃ�ق��A�C�ݕt�߂̐��[���[���Ȃ邽�߁A�g���ӂ��ăG�l���M�[�������u�Ӕg�v�Ƃ������ۂ��N����ꏊ���Z��n�ɋ߂��Ȃ�A�g�����B����댯�������܂�Ƃ������Ƃł��B
�@����A���l�����鉓��̊C�݂ł́A�C�ݐ����Z��n���牓���Ȃ�ق��A�u�Ӕg�v�������ŋN���邽�߁A�g�����B���ɂ����Ȃ�Ƃ������Ƃł��B
�@�L�싳���́u���l���Ȃ��Ȃ�ƁA�g���Ȃ��Ȃ��ӂ����ɗ��n�ɓ��B���A�Z��̑������ꂽ��ǂ���ꂽ�肷���Q���\���N���肤��Ǝv���B���l���h�Џ�厖�Ȗ�����S���Ă��邪�A����A�n�����g�����i�ނƊC�ʂ̏㏸�ō��l���Ȃ��Ȃ邱�Ƃ��l������̂ŁA���l������Ă������Ƃ����ɏd�v���v�Ƙb���Ă��܂����B
�H��ɂ��e��
�@���l�̏����⌸���́A�C�̐��Ԍn��ω������A�������̐H��ɂ��e�����y�ڂ��\��������Ǝw�E������Ƃ����܂��B
�@���Y��w�Z�̐{�c�L�㋳���ɂ��܂��ƁA���l�́A�������́u���u�v�ƍ��u�ƊC�̊Ԃ́u�l�v�A����ɔg�ł��ۂ���ɂ����Ắu�T�[�t�]�[���v�̂R�̃G���A�ɕ��ނ����Ƃ������Ƃł��B
�@���̂����A�u�l�v�Ȃǂ̉���ʂ��ĊC�ɗ��ꍞ�ޒn�����ɂ́A�A���v�����N�g���̉h�{�����L�x�Ɋ܂܂�Ă��܂��B�܂��A�g�ł��ۂɂ́A�ł��グ��ꂽ�C���Ȃǂ�����ɕ��ԁu�h���t�g���C���v���`������A�����̐������́u�B�ꂪ�v�ƂȂ��Ă��܂��B
�@����ɁA�g�ł��ۂ��܂ށu�T�[�t�]�[���v�ɂ́A�v�����N�g���̂ق��A�u�A�~�v��u���R�G�r�v�Ȃǂ̏����Ȑ��������������������A�����_���āA�����̋��̒t�����W�܂��Ă���Ƃ������Ƃł��B
�@�{�c�������A��w�ɋ߂��R�������֎s�́u�T�[�t�]�[���v�������Ƃ���A�q������V���M�X�A����ɃX�Y�L�̒��ԂȂ�60��ވȏ�̒t����������A��U�������ʁA�݂̒�����u�A�~�v��u���R�G�r�v�Ȃǂ����������Ƃ������Ƃł��B
�@���̂����A�q�����́A���N�t�ɑ̒��R�Z���`�قǂ̒t�����u�T�[�t�]�[���v�ɂ���Ă��āA��P�N�����āu���R�G�r�v�Ȃǂ�H�ׂĐ������A15�Z���`�O��ɂȂ�Ɖ����ɏo�čs�����Ƃ��������Ă��āA�������Ĉ�����������Ƃ̑ΏۂɂȂ�Ƃ������Ƃł��B
�@���̂悤�ɍ��l�́A�����̒t���̉a���������Ă��邱�Ƃ���A�{�c�����́A���l�������Ă��܂��Ɛ��Ԍn�̃o�����X������A�������̐H��ɂ��e�����y�ڂ��\��������Ǝw�E���Ă��܂��B
�@�{�c�����́u�q�����Ȃǂ��Ŏq�ǂ��̎��ɂ�������Ɖa��H�ׁA�傫���炽�Ȃ���A���Ƃ͐������Ȃ��Ȃ�B���l�́A���ڂ̋���ɂ͂Ȃ�Ȃ����Ȃ��Ȃ��Ă��܂��ƁA�ŏI�I�ɂ͐l�Ԃ̐����ɂ��e�����o��Ƃ������Ƃɂ��Ȃ���B���l�̑�������З������Ăق����v�Ƙb���Ă��܂����B
���Ɓu���炩�̑� ��ΕK�v�v
�@���g�ɂ��ЊQ��n�����g�����C�݂ɗ^����e���Ȃǂɏڂ������m�H�ȑ�w�̈镔��F�w���́A�����_�ō��l������������A���������肵�Ă��錴���́A���̋}���ȊC�݊J���̐i�W�ɂ����̂ŁA���s���Ă����́A���g���������������̂ł͂Ȃ��Ǝw�E���Ă��܂��B
�@���̂����ŁA�镔�w���́u���l�����邱�Ƃɂ���āA�傫�Ȕg�����ōӂ��Ĕ�Q��h���Ƃ����h�Џ�̌��ʂ����邵�A���Ԍn�̖ʂł��A�C������T�[�t�B���Ȃǂ̃��N���G�[�V�����̏�Ƃ��Ă��d�v�ȏꏊ���B���l�̐Z�H�́A�������Ԃ������ċN����̂ŁA���ڂ��W�߂�@����Ȃ����A����A���g���ō��l���������茸�����肷�邱�Ƃ͂قڊm���Ȃ̂ŁA���炩�̑��ł��Ƃ͐�ΕK�v���v�Əq�ׁA����́A���g���̐i�s�������������V���ɍs���K�v������Ƒi���Ă��܂��B
�@���̕��A�O�l�̓T�^�I�ȃt�F�C�N�j���[�X�ł��B
�@���g����������n�߂�����A����ɂ̕X���������ĊC�ʂ��㏸����A����̉ʂĂɂ͖k�ɊC�̊C�X�������ĊC�ʂ��㏸����ȂǂƂ����A���w���ł����o�������ȃo�J�����������}�X�R�~�ł��B���{�̍��l��������Ƃ����b���A���������Ԃ�O�ɕ������o��������܂����A�����܂��Ă������̋��|��`�Ƃ́A����܂���(��)�B���̐}�́A�ȑO�×�����IPCC2013�N�̊C�ʏ㏸�̗\���}�ł��B
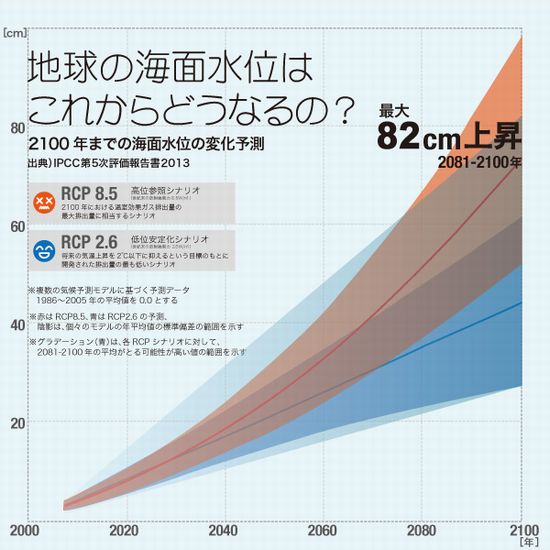
�@����̕ł́A4���㏸�ɂ��Ă͈���̉Ȋw�I�ȗ��t��������ɂ��Đ����͂Ȃ��A�����P�Ɂu�����I���܂łɐ��E���ϋC��������4���オ������v�Ƃ������ݒ�ɑ��āA�u�C�ʂ�60cm�㏸���邩������Ȃ��v�Ƃ����A���̗��t�����Ȃ��ɋ��|�S����邾���́u�ˋ�́��������v����A�u�����ȃt�F�C�N�j���[�X�v�ł��B��l���Ȃ��Ƃ��v���܂���(��)�A�����R�����g���Ă����܂��傤�B
�@�܂��A4���̋C���㏸�Ƃ����̂́A���Ȃ�ȑO��IPCC�̕��ɂ����鉷�g���V�~�����[�V�����̍ň��P�[�X�Ȃ̂ł͂Ȃ����Ǝv���܂��B�ߍ��͂����܂ŋɒ[�ȋC���㏸���������Ă�̂͒��������Ƃł��B���������̋Z�������́A���g����̐��������咣���邽�߂ɌÂ��f�[�^�Ɋ�Â��āA��Ԑ����̍��l�����������o�����Ƃ����Ƃ���ł��B
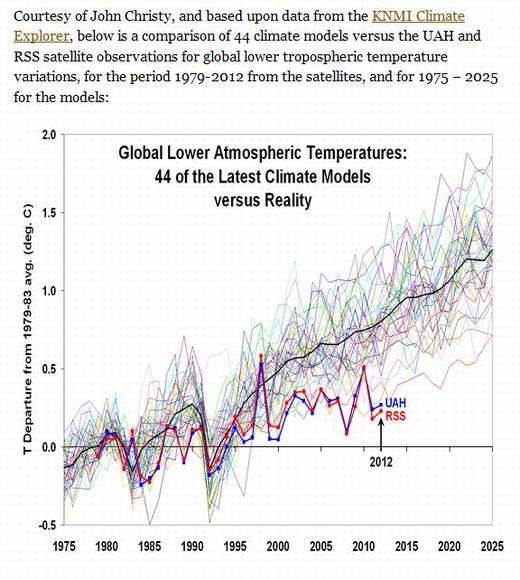
�@�Ⴆ�Ώ�}�Ɏ����悤�ɁA���l�V�~�����[�V�����̌��ʂ�2000�N��ɓ����Ă����E���ϋC���͒P���ɏ㏸����Ɨ\������Ă��܂����A���ۂ�UAH��RSS�̊ϑ��l��2000�N��ɓ����Č����ȏ㏸�X���݂͂��܂���B
�@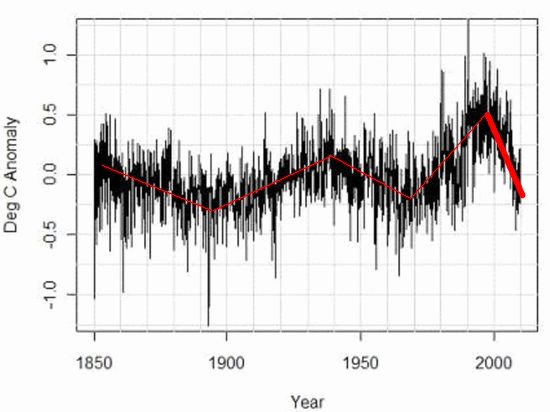
�@��}�́AGHCN�̊ϑ��X�e�[�V�����̖���f�[�^�̐��E���ϋC���������������̂ł����A2000�N��ȍ~�A�}���ȋC���ቺ�ǖʂɓ����Ă����Ƃ����̂�����ł��B�����I����4���㏸�ȂǂƂ����r�����m�ȉ���͂܂����������I�ȈӖ��͂Ȃ��A��O��k�ɕs���Ɋׂ�邽�߂̃t�F�C�N�ł��邱�Ƃ͘_��ւ��܂���B
�@���݂͕X�͊��̑����ɂ���܂��B�X�͊��i���Ɋ��⍂�R�ɕX�͂����݂��鎞���j�̒n���̋C���́A���`�I�ɑ��z�����ɂ���ĕϓ����܂��B
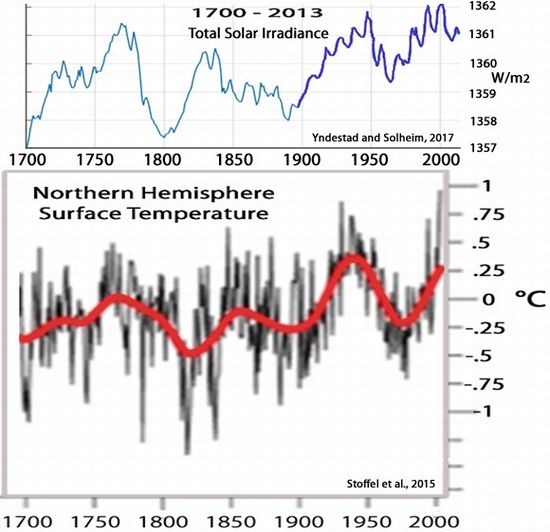
�@��}�́A����1700�|2000�N�̑��z���ˏƓx�iTotal Solar Irradiance�j�Ɩk�����̋C�������r�������̂ł��B���z���ˏƓx�̕ϓ��Ɩk�����̋C�����̕ϓ��ɋ������̑��֊W�����邱�Ƃ��킩��܂��B
�@2000�N��ɓ����Ă���C�����ቺ�ǖʂɓ��������Ƃ́A���z�����̊����x�̒ቺ���疾�炩�ł��B���̐}�͍ŋ߂̍��_���ΐ��̊ϑ����ʂł��B
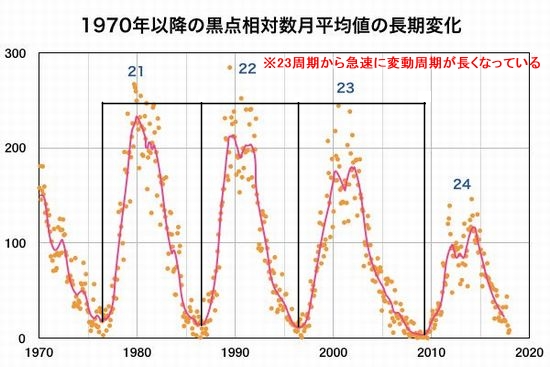
�@���z���_���ΐ��Ƒ��z���ˏƓx�ɂ͋������֊W������܂��B���}�͐���1975�|2015�N�̊��Ԃ̑��z���ˏƓx�Ƒ��z���_���̕ϓ��X���������Ă��܂��B
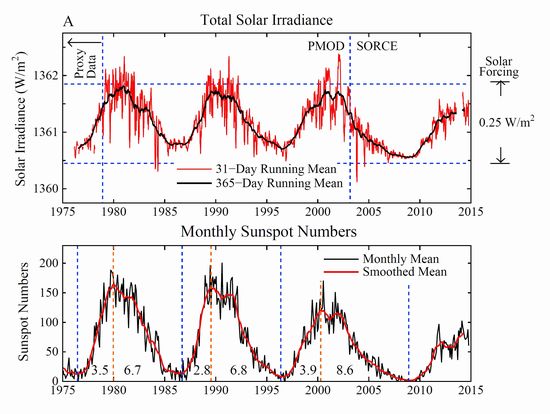
�@�܂��A���z���_���ΐ��̕ϓ��������Z���قǑ��z�����͊����ł��B20���I�̑��z���_���ΐ��̕ϓ������͕��ς����11�N�قǂł����B�`���[���b�q�ԍ�21�A22�ł͕ϓ�������10�N���x�ł���A���z�����������ł��������Ƃ��킩��܂��B��]���āA1997�N����̎�����12�N���Ă��܂��B���z�����̒ቺ�����炩�ł��B�܂��A2009�N����̎����ł͂���ɑ��z���_���ΐ��̔��������Ȃ��A�����ĕs����ɂȂ��Ă��Ă���A������12�N�������ł��B
�@���ɁA20���I�I�ՁA1980�N�ォ��2000�N�ɂ����Ă̋C���㏸�ɂ���āA��ɕX�����Z�����ĊC���ʂ��㏸����Ƃ����������������̂��A�Ƃ����_�ɂ��Ă݂Ă����܂��傤�B
�@�����m�̂悤�ɓ�ɕX���Ƃ͓�ɑ嗤�ɍ~�����Ⴊ�A��N���X�_���̓�ɂ̊����ŗn���邱�ƂȂ�����̏d���ʼn����ł߂��Ăł������̂ł��B���������āA�X���̐������x�͍~��ʂɔ�Ⴗ��ƍl�����܂��B
�@���āA���{�̖k�����瓌�k�̓��{�C���͐��E�̍���n�тł��B�C���̒Ⴂ�ꏊ�͑��ɂ�������ł�����܂����A���������ł͍~��ʂ͑����Ȃ�킯�ł͂Ȃ��A��ʓI�ɂ͂ނ���~��ʂ͏��Ȃ��Ȃ�܂��B�Ⴊ�����Ȃ��C���ł���A�o���邾�������ł�������A���z�������ō~��ʂ͑����Ȃ�܂��B
�@���������āA�N�ԕ��ϋC�����|10����A���邢�͂�������Ⴂ��ɑ嗤�ł́A�C�����㏸��������~��ʂ������Ȃ�A���������āA�X���̐��Y�ʂ͑��������̂ł��B����𗠕t����悤�ɁA2015�N11���ANASA�ɂ���ɕX���̊ϑ����ʂ��Ȋw���uJournal
of Glaciology�v�Ɍ��J����A���̕ł́A1992�`2001�N�̊��Ԃ͕��ς����1120���g��/�N�̃y�[�X�ŕX�����������A2002�`2008�N�̊��Ԃ�820���g��/�N�̃y�[�X�ő��������Ƃ��Ă��܂��B
�@�܂��A���Ȃ��Ƃ�20���I�㔼�ɂ͓�ɑ嗤�͊��≻���Ă���A�C�X�ʐς��������Ă���̂ł��B
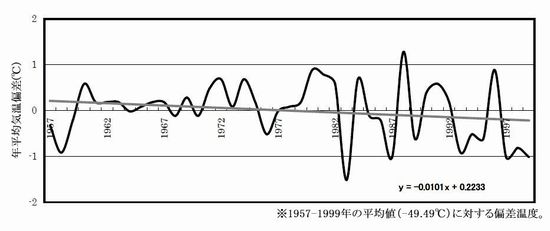
�@���̐}�͓�ɑ嗤���ӕ��Ɉʒu������{�̏��a��n�̋C���ω��ł��B��A�����̌X���́|0.0042��/�N�ł��B
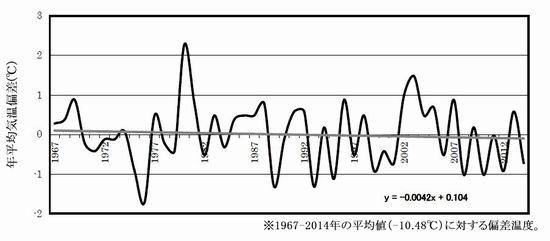
�@���̐}�́A��ɑ嗤���S���ɋ߂��T�E�X�|�[����n�ł̋C���ϑ����ʂł��B������́|0.0101��/�N�ł��B
�@���̐}�́A��ɊC�̊C�X�ʐς̕ω��ł��B1980�N������̊ϑ����Ԃ�ʂ��đ����X���������Ă��܂��B�C�X�͊C������p����ĕX�ɂȂ���̂ł�����A��ɊC���ӊC��ł͋C�����ቺ�X���ɂ��邱�Ƃ������Ă���ƍl�����܂��B
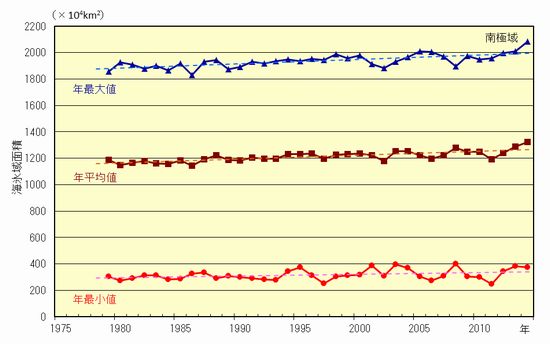
�@�ȏ�̎�������A20���I�I�Ղ̋C���㏸���ɂ́A��ɕX���̑̐ς͑������A��������ɑ嗤�y�т��̎��ӊC��̋C���͒ቺ�X���������Ă����̂ŁA��ɕX�����Z�����ĊC�ʂ��㏸����Ƃ������ۂ͑��݂��Ȃ������̂ł��B
�@�ȏ�A�������Âɔ��f����A�����I���܂łɐ��E���ϋC����4���㏸���ĊC���ʂ�60cm�㏸����ȂǂƂ������Ƃ͖ϑz�Ȃ����͈����ȃt�F�C�N�j���[�X�ł���ƒf���ł���̂ł��B
No.1246 (2018/12/10) �C�ۃV�~�����[�V�����Ō����̋C�ی��ۂ��ؖ��H�I
�C�ۃV�~�����[�V�������C�ی��ۂ𐳂����͕�ł���ۏ͑��݂��Ȃ�
�@12��7����NHK�̒��̃j���[�X�ԑg�ŁA����̃`�[�������N�̉Ă̖ҏ������g���̉e���ł��邱�Ƃ��A100�ʂ�̋C�ۃV�~�����[�V�������s�������ʁA�ؖ������ƕ��Ă��܂����B�܂��͂��̕ɂ��Ă�NHK�̃E�F�u�T�C�g�̋L�����Љ�Ă����܂��B
�@�@�����ŋN���Ă���ُ�C�ۂɒn�����g�����{���ɉe�����Ă���̂��B���Ƃ��̋L�^�I�Ȗҏ��ɂ��āA���Ƃ����g�����i��ł��Ȃ��Ɖ��肵�ĉ�͂����Ƃ���A�����悤�Ȗҏ��ƂȂ�m���͂قڂO���ŁA���g���̊m���ȉe�����ؖ�����܂����B
�@�@���Ƃ��̉ẮA��ʌ��F�J�s�̋C�����A�ϑ��j�㍑���ōł�����41�x�P���ɒB�����ق��A�����{�̕��ϋC�������v�����n�߂Ă���ł������Ȃ�ȂNjL�^�I�Ȗҏ��ƂȂ�܂����B
�@�@����ɂ��ċC�ے��̌�����́A�u���L�̋C���z�u�≷�g���ɂ�钷���I�ȋC���̏㏸�X�����e�������v�ƌ��_�Â��܂������A���ۂɉ��g�����ǂ̂��炢�e�����Ă����̂��ؖ�����Ă��܂���ł����B
�@�@������w��C�C�m�������ƋC�ے��C�ی������̌����`�[���͎Y�Ɗv���O�̉��g�����i��ł��Ȃ��ꍇ�̋C�ۏ����݂܂ő����Ă���Ɖ��肵�������ŁA���Ƃ��̋L�^�I�Ȗҏ����������邩�ǂ����m������͂��܂����B
�@�@���̌��ʁA�C���z�u�̉e���ŕ��N�ɔ�ׂč����ɂȂ�₷���������̂́A���g�����i��ł��Ȃ�����Ƃ��V���̏��̋C���͂��悻�Q�x�Ⴍ�Ȃ�A���Ƃ��̂悤�ȋL�^�I�Ȗҏ�����������m���͂قڂO���ŁA���g�����m���ɉe�����Ă������Ƃ��ؖ��ł����Ƃ������Ƃł��B
�@�@����܂ňُ�C�ۂɂ��ẮA�w�i�ɉ��g���̉e��������Ǝw�E����Ă������̂́A�ʂ̌��ۂƂ̊W�����ۂɏؖ����錤���͎n�܂�������ŁA��̓I�ȉ��g����̎肪����ɂȂ�Ƃ��Đ��E�I�ɒ��ڂ���Ă��܂��B
�@�@������w��C�C�m�������̓n����_�����́A�u����܂ʼn��ƂȂ������킩��Ȃ��������g���ƈُ�C�ۂ̊W���ؖ����邱�Ƃ��ł����B������i�߂邱�Ƃňُ�C�ۂ��N���郊�X�N�����ۂɂǂꂭ�炢����̂��A�m�����o����悤�ɂ������v�Ƙb���Ă��܂��B
���g���̉e����T��V��@�Ƃ�
�@�@�����ɋN�����ҏ��⍋�J�Ƃ������ُ�C�ۂɁA���g���̉e�����ǂ̂��炢�������̂����ؖ����邽�߁A������w�̓n��������̌����`�[������͂Ɏg���Ă����@�́A�u�C�x���g�E�A�g���r���[�V�����v�ƌĂ�Ă��܂��B
�@�@���̌�����@�́A�Y�Ɗv���O���牷�g�����i��ł��Ȃ��n�������肵�������ŁA���g�����i�����̒n���Ɣ�r���邱�ƂŁA�ʂُ̈�C�ۂɉ��g�����^�����e�����ؖ����Ă�����@�ł��B
�@�@�������ʃK�X�̔Z�x��C�ʐ����Ȃǂ̃f�[�^�����100�ʂ�̃V�~�����[�V�������s���āA�C�����C���̐����C�ʂȂǂ���͂�����ُ̈�C�ۂ��N����m���Ȃǂ��v�Z���������Ŕ�r���܂��B
�@�@������w�̓n�������ɂ��܂��ƁA�u�C�x���g�E�A�g���r���[�V�����v���g������܂ŌX�̋C�ی��ۂɂ��Ă͂����莦�����Ƃ��ł��Ȃ��������g���̉e���ɂ��āA���l��p���ďؖ����邱�Ƃ��ł��邽�߁A��̓I�ȉ��g����ɂȂ���Ƃ��Đ��E�I�ɂ����ڂ���Ă���Ƃ������Ƃł��B
�����{���J�̉J�� ���g���̉e���ő���
������w�̓n��������̉�͂ł́A���Ƃ��̐����{���J�̉J�ʂ��A���g���̉e���łU���قǑ������Ă����\�����������Ƃ��������܂����B
�@�@�n��������́A�U��28������V���W����Ώۂɋ�B���瓌�C�ɂ����Ă̒n����T�L���l���ɕ����āA���g�����i��ł��Ȃ��Ɖ��肵���ꍇ�̉J�ʂƁA���g�����i��ł��錻���̋C�ۏ����Ƃɉ�͂����J�ʂ��r���܂����B
�@�@���g�����i��ł��Ȃ��Ɖ��肵���J�ʂ́A1980�N�ȍ~��20�N�Ԃŏ㏸�����C����A����ɂ���đ���������C�̐����C�ʂ����������������ŃV�~�����[�V�������܂����B
�@�@���̌��ʁA�ϑ��_���Ƃ�11���Ԃ̑��J�ʂ̕��ς͉��g�����i��ł��Ȃ��ꍇ��252.3�~���������̂ɑ������̋C�ۏ����Ƃɉ�͂����J�ʂ�267.9�~���ƁA���g���̉e���ʼnJ�ʂ��U���قǑ������Ă����\�����������Ƃ��킩��܂����B
�@�@����̍��J�ɑ��A���g�����ǂꂭ�炢�e�����Ă������������͍̂����߂Ăł��B
�@�@�n�������́u�U�������Ƃ����Ƃ������������ł͂Ȃ��悤�������ꂾ���J�ʂ������グ���ꂽ���Ƃɂ���Ă�苭���J���L��ő������ƂɂȂ������ƍl���Ă���v�Ƙb���Ă��܂��B
�@�@���ɂ���͓T�^�I�ȁA�R���s���[�^�[���g�����s��ȃt�F�C�N�j���[�X�ł��B�L�������Ă���������̒ʂ�A�ǂ̂悤�ȏ����ŃV�~�����[�V�������s���ċ�̓I�ɉ����ǂ̂悤�ɂȂ邱�Ƃ������������ʁA���R�Ȋw�I�Ɍ��Ă��̉Ă̓��{�̖ҏ��ɂǂ̂悤�ɐl�דI�ȉ��g�����e�������̂����ؖ����ꂽ���Ƃ����_�ɂ��āA��̏����܂���B���g���������݂̒n���Ɖ��g�����Ȃ������ˋ�̒n���Ƃ̈Ⴂ�͂����������Ȃ̂��H������ǂ��ؖ������̂ł��傤���H
�@�������āA���̕\������ʂ����߂ĕ��������C�ɂȂ�命���̑�O�̔]���ɂ́A�C�ۃV�~�����[�V�����͂��ɋC�ی��ۂ��ؖ����邱�Ƃ��ł���悤�ɂȂ����̂��A�����āA���̉Ă̖ҏ��̌����͐l�דI�Ȓn�����g���̌��ʂȂ̂��A�Ƃ������Ƃ��������Ƃ��č��荞�܂�Ă����̂ł��B���̎�̌������ʂɂ��ẮA��ʑ�O�ɂ͌��̎�i���Ȃ��̂ł�����A����u���������̏����v�ł��B���ɂ͂���قǓs���̗ǂ����̂͂���܂���B���̂悤�ȕ̎d��������NHK�Ƃ������@�ւ͐��ɍߐ[���Ƃ���˂Ȃ�Ȃ��ł��傤�B
�@�@���������A�C�ۃV�~�����[�V�����ȂǂƂ�����������ŋC�ی��ۂ��Č�����\�͂��ؖ����ꂽ�ȂǂƂ����b�������Ƃ�����܂���B����Ȃ��̂Ō����̋C�ی��ۂ̎d�g�݂��ؖ�����ȂǁA�y�䂠�蓾�Ȃ��b�ł��B�ƂĂ��P���Șb�ł����A���{�̍Ő�[�̋C�ۃV�~�����[�V�����Ɋ�Â����C�ۗ\���ł����Ă��A��T�Ԑ�̓V�C�\�����邱�Ƃ͂���܂���B����̋Z�p��150�N�̃^�C���X�p���ɑ��Ă܂Ƃ��ȗ\�����ł���ۏȂǂȂ����Ƃ͕�������Ă��܂��B����ȏ�̐����͕K�v����܂���B
�@�@���̂����ŁA����̕ɂ��đ����R�����g���q�ׂĂ����܂��B���ʂ�5km�l���̃��b�V���Ƃ́A�����Ԃ�Ƒ�G�c�ȉ�̓��f���ł���A���͂��ꂾ���ł�����̃V�~�����[�V�����͗^���b�ł���A�]���ɒl���Ȃ��ƍl���܂��B������100�ʂ���̉�͂��s�����Ƃ́A�v����Ɍ����̋C�ی��ۂ��u���m�̃R�g�����v�Ƃ��Ď��R���ۂƂ��Ď����ȃ��f�������ł��Ȃ�����A����ȓS�C���������ᓖ����ł͂���܂���(��)�A�R���s���[�^�[�Ȋw�҂ɂ�霓�ӓI�Ȏv���t���́u�d�|���v�����ʂ���v�Z���Ă݂܂����Ƃ������Ƃɂق��Ȃ�܂���B
�@�@��̋C�ی����҂����͂��܂ł��̂悤�ȕs�тȂ��V�тɋ��������Ȃ̂ł��傤���H�u����Ȃ��Ƃ����Ăėǂ��̂��v�ƍl����܂Ƃ��Ȍ����̋C�ی����҂͂��Ȃ��̂ł��傤���B
�Q�ƁF
No.1244�@�i2018/11/14�j
���̗͊w�V�~�����[�V�����̓K�p���E���l����C
�@�C���\���V�~�����[�V�����͗��̗͊w�������̓K�p���E����E���Ă���
No.1245 (2018/11/22) �����Ɛl�דI���g���E�ăG�l�̋��χA
�u�����v���l����A�Ƃ͂ǂ��������Ƃ��H
�@����́A���߂Ċ������l����Ӗ��Ƃ͉��Ȃ̂��ɂ��Đ������Ă��������Ǝv���܂��B
�@�܂��A�n���j�I�ɂ݂āA���݂̐l�ԎЉ�̓��ꐫ�ɂ��ĊT�ς��Ă������Ƃɂ��܂��B
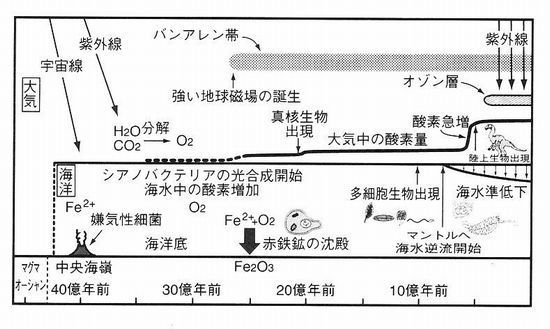
�@35���N�قǑO�Ɍ������������o�ꂵ�A�C�����Ɏ_�f���������n�ߊC�����̓S�C�I���͎_���S�ƂȂ�S�z�����`����܂����B��������_�f�͊C�����̓S�C�I�����_���������A�₪�đ�C���̎_�f�Z�x�������Ȃ�n�߂܂����B�����n������̒a���ƁA��C���_�f�̑����ɂ��I�]���w�̌`���Œn�\�ʂɓ��B����F�����⎇�O���ʂ������������ʁA5���N�قǑO�ɗ��㐶�����o�����܂����B
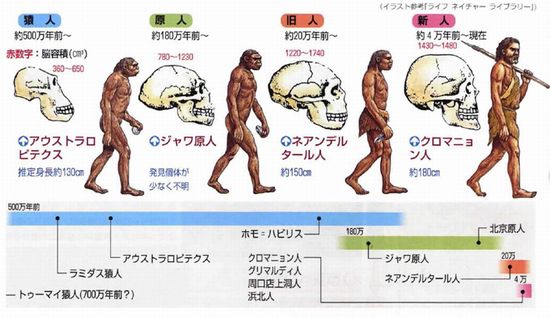
�@�l�ނ̒��n�̐�c�ƍl�����鉎�l��500���N���O�ɓo�ꂵ���ƍl�����Ă��܂��B���傤�nj��݂ɑ����X�͊����n�܂�������ł��B���l�A���l���o�āA���݂̐l�ނ̒��ڂ̐�c�ƍl������V�l���o�ꂵ���̂́A�킸��4���N�قǑO�̂��Ƃ��ƍl�����Ă��܂��B����͑O��̕X���̂������ł����B
�@���Ɏ����}�́A�O�X�����猻�݂̊ԕX���̋C���ϓ��̊T���i���ۂɂ͑�C���̎_�f���ʑ�18O�䗦��1000�����j�Ɛl���A�G�l���M�[����ʂ̐��ڂ������Ă��܂��B
�@�ŏI�X���̏I����������1��2000�N�O�̐��E�l���͐�100���l���x�ł������ƍl�����Ă��܂��B�����N�̐���l����2���l����3���l���x�ƍl�����Ă��܂��B����1000�N���܂ł͐l���͑Q�����A���̌��C�ɐl�����������n�߂܂����B����18���I�̎Y�Ɗv���ȍ~�͋}���Ȑl�������������Ă��܂��B�܂��A�@�Y�Ɗv���ȍ~�A�ΒY�A�Ζ����͂��߂Ƃ��鉻�ΔR���𒆐S�Ƃ���H�ƓI�ȃG�l���M�[����}�����Ă��܂��B
�@�������l�ԂƂ�����r�I��^�̓�����̋ߔN�̒Z���Ԃ̔����I�Ȑl���������ۂ́A���R�E�ł͂܂�Ȍ��ۂł��낤�ƍl���܂��B
�@���̗v���́A�ŏI�̕X����1��2000�N�قǑO�ɏI���A���̌�C���ϓ��̏����Ȉ��肵�����g�����p�����Ă��邱�Ƃ��������܂��B���̌��ʁA���Ԍn�̈ꎟ���Y�҂ł���A���̐���\�Ȓn�悪�L����A���Y�����������傫���Ȃ����̂ł��B
�@���̗v���́A�C���肵�����ʁA�_�k���J�n����v��I�ȐH�����Y�E���Y�A�����ė]��H�Ƃ̔��~�ɂ���ĐH�����Y���������ꂽ�W�c�ɂ���ĉȊw�Z�p�����W�𐋂��A�_�k���������������Ƃł��B
�@�����đ�O�̗v���́A�~�ς��ꂽ�Ȋw�Z�p�ɂ���ĉ��ΔR����p�����M�@�ցA���͋@�ւ���������A����܂łɒ~����ꂽ�Ȋw�Z�p�A���Y�Z�p�Ɠ��͋@�ւƂ��������邱�ƂōH�ƕ������N����A�l�ԎЉ�̐��Y��������I�ɑ傫���Ȃ������Ƃł��B
�@�l�ԂƂ���������̌��݂̔ɉh�̓��ِ��́A���A��O�̗v���A�܂�l�Ԃ����x�ȎЉ�������A����⎑���𗘗p���Ȃ�����ɑ��ĐϋɓI�ɓ����������s���Ă���_�ł��B���ɑ�O�̗v��������1000�N�ȍ~���݂܂Ōp�����Ă��锚���I�Ȑl�������̎�v�ȗv���ł��B
�@���݂́u�l�ނ̔ɉh�v�͊��V���̉��g�ň��肵�������ȊԕX���̓���ȏ������ŐH�Ƃ̑��Y��w�i�ɁA��C�Ɋg�債�����̂ŁA���̂悤�ɒP��̔�r�I�傫�ȓ����킪�ɋ}���ɐ��������邱�Ƃ́A�ɂ߂Ĉٗ�Ȃ��Ƃł��B����s���ɔC���Ă��܂��A�l�ԎЉ�ɉh�̊�ՂƂȂ�H�Ɛ��Y�\�͂̌��E�Ƃ���ɔ������E�I�_�n�̍������ɂ���āA�����炭�����Ȃ������ɏI���Ɍ������j�ǓI�ȕ��n�܂�ƍl�����܂��B
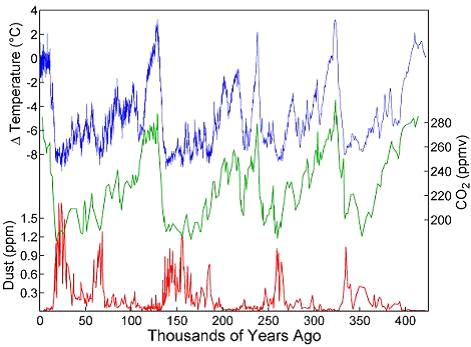
�@��}�͓�ɕX���R�A�̕��͂��狁�߂�ꂽ�ߋ�40���N�]��̊��Ԃ̋C���A��C��CO2�Z�x�A���o�ʂ̌o�N�ω��������Ă��܂��B�}���番����悤�ɖ�10���N�̎����ő��ΓI�ɋC���̒Ⴂ�X���ƁA���ΓI�ɒg�����Z���Ԃ̊ԕX�����J��Ԃ���Ă��܂��B������������炵�Ă���̂͐}�̍��[�̊ԕX���̏I�Ղ��ƍl�����܂��B���݂̊ԕX���͂����炭�߂������ɏI�����}���A����Ō������C��ϓ����X���Ɍ��������Ƃ͔������܂���B
�@�t�������Ă����ƁA��}������Ɗ�����ɂ͕��o�ʂ̑������݂��܂��B����́A�C���̒ቺ�ɔ����Đ��z���ቺ���A�~���ʂ��������邱�ƂŒn�\�ʊ������������邱�Ƃ��������Ă��܂��B���≻�͂��ꂾ���Œn�\�ʊ��̍�������i�s������v���ɂȂ�܂��B�H�����Y�̕N���ɂ����E�I�_�n�̍��g�Ɗ��≻���d�Ȃ�ƁA�������ɂ��H�Ɛ��Y��Ղ̕���͋}���ɐi�މ\���������ƍl�����܂��B
�@���݂̕����͍H�ƓI�ȃG�l���M�[�̑�ʏ���Ɏx����ꂽ����߂ē���ȕ����ł���A�������X�����o���������Ƃ�����܂���B���݊m�F����Ă���G�l���M�[�����̖̉����ʂ́A���݂̐����ŏ���𑱂����1000�N��҂����Ɍ͊����邱�ƂɂȂ�܂��B
�@�������̎q�������͔ۉ��Ȃ��A�|�X�g�H�ƕ���������Ȃ��̂ł��B�ނ�͊���Ō������C��ϓ���10���N�߂��p������ƍl������A����ׂ��X���̑唼�̊��Ԃ��H�ƓI�ȃG�l���M�[����Ȃ��ʼn߂������Ƃ��K�v�ɂȂ�̂ł��B
�@�����ŁA�l�ԎЉ���������I�ɐ������т邽�߂ɂ́A�H�ƓI�ȋZ�p�ɉߓx�ɗ���Ȃ��A��ɒn���̐��Ԍn�̒��ōX�V�I�ɓ����鎑���Ől�ԎЉ������I�Ɉێ����邽�߂̎d�g�݂��\�z���邱�Ƃ��K�v�ł��B���̂��߂ɁA���݂̍H�ƕ����Љ�̎����E�Ɩ��_�𖾂炩�ɂ��A����ׂ�����������т邽�߂̐l�ԎЉ�̐����헪���l���邱�Ƃ��K�v�ł���A���ꂪ�������l����Ƃ��������Ȃ̂ł��B
�@���̃z�[���y�[�W�ʼn��x���G��Ă��܂����A���͊������l�����ł̑�O��Ƃ��āA��Ε��a��`���Ƃ�܂��B����̐����̂��߂ɂ͎�����H�̎E�������F����Ƃ����̂ł���A�H�����Y�̌����ɔ����Đ��S�ȌR���N�U�ɂ��\�͓I�Ȑl�������ɂ�鍬���ƍX�V�������̐��Y�̏�ƂȂ�ׂ��n�\���̍r�p���s�����ƍl���邩��ł��B�����ł͂Ȃ��A�L���̎������������A���Ԍn�̍X�V�������̐��Y�\�͂Ɍ��������K�́A�V�X�e�������l�ԎЉ�Ƀ\�t�g�E�����f�B���O���邽�߂ɂ����A�������l����Ӗ�������Ǝv���܂��B
�@���̓_�ɂ��ẮA�M�����w�҂̒Ɠc�ւ���̒����u�V�Ζ������_�v�i2002�N�A�_�����A129�Łj�̋L�q���Љ�Ă��������Ǝv���܂��B
�@3�D���≻�ŋ��낵���̂͐N���푈
�@�������́C�l�Ԃ̍s�ׂɂ���Ă����炳�ꂽ���̂ł��邩��C�l�Ԃ̑�ʼn������邱�Ƃ��ł���B�������C���≻�͐l�Ԃ̗͂ł͖h�����Ƃ͂ł��Ȃ��B�n���̋C�ۂ�ς��悤�Ƃ���w�͂͐l�Ԃ̂�����ł���B�Ñ㕶���ɂ����āC�u�o�x���̓��v�̓`�������ۂɂ������b�ł͂Ȃ��ɂ��Ă��C�����̐l�X���V���ς��悤�Ƃ����C���������������Ƃ̏؋��ł͂���B���݂ł́C�����̐l�X�͋C�ۂ�ς������Ɗ肢�C�u�n�����g���h�~�v�Ƌ���Łu�V�Ɍ������đ�����v�s�ׂɈꐶ�����ɂȂ��Ă���B
No.1237�@�i2018/10/17�j
�����Ɛl�דI���g�����E�ăG�l�̋��χ@
No.1239�@�i2018/10/24�j
�����Ɛl�דI���g�����E�ăG�l�̋��ρ@�ԊO��
No.1249�@�i2019/01/11�j
�����Ɛl�דI���g�����E�ăG�l�̋��χB
No.1244 (2018/11/14) ���̗͊w�V�~�����[�V�����̓K�p���E���l����C
�C���\���V�~�����[�V�����͗��̗͊w�������̓K�p���E����E���Ă���
�@���āA�A�ڂ�4��ڂɂȂ�܂����̂ŁA�ꉞ����̘A�ڂ̂܂Ƃ߂��s���Ă������Ƃɂ��܂��B���w�I�A���邢�͕����w�I�Ȍ������ɂ͑����ڂ��Ԃ��Ă��������āA�Ȃ�ׂ��N�ɂł������ł�������ɂȂ�悤�ɂ������Ǝv���܂��B
1.�@���I�ȋC�ی��ۂ̗\���ɑ��āANavier–Stokes��������K�p���邱�Ƃ͂ł��Ȃ��B
�@����ɂ͂������̗��R������܂��B
�@�O��̎��^�����ŏЉ���Ƃ���ANavier-Stokes�������͔S�����̂ɑ���j���[�g���̉^���������̋ߎ����ł��B�j���[�g���̉^���������̑�O����v���o���Ȃ���Ȃ�܂���B�j���[�g���̉^���������������n�ɂ��������_�̉^���Ɨ͂̊W�����������̂ł��B
�@�����n�Ƃ́A�����̖@���A���Ȃ킿�u�͂��Ȃ����͉̂i���ɐÎ~�������邩���������^���𑱂���v�悤�ȋ�Ԃł��B�܂��A���_�Ƃ͎��ʂƋ�ԓI�Ȉʒu��������`���ꂽ�̐ς������Ȃ����z�̓_�ł��B
�@�Ƃ��낪�A�n���͋�͌n�̊O���ɋ߂����z�n�ɑ�����f���ł��B��͌n�͉F���̂ǂ����ɂ��邩������Ȃ���ΐÎ~�n�̒��S�ɑ��Č��]���Ȃ��玩�]���Ă��܂��B����ɑ��z�n����͌n�̒������]���Ȃ�����]���Ă��܂��B�X�ɒn���͑��z�̎�������]���a��n���̌X����ʑ���ω������Ȃ�����]���Ȃ��玩�]���Ă��܂��B���������āA�n���ɌŒ肳�ꂽ���W�n�͐���W�n�⊵�����W�n�ɑ��Ĕ��ɕ��G�ȉ����x�^������������x���W�n�ɂȂ�܂��B���������āA�����ɂ͒n����ł̓j���[�g���̉^���������͐��藧���܂���B
�@�Ƃ͂����ANavier-Stokes���������S�����ɗ����Ȃ��킯�ł͂���܂���B���ɂȂ��Ă���̂͒n���ɌŒ肳�ꂽ���W�n�������x���W�n�ł���A�n���ɌŒ肳�ꂽ���W�n�ŋL�q���ꂽ�^���ɂ͊����n�ŋL�q�����^���ł͓����Ȃ��͂��̉��z�̗͂ł��銵���́i�Ⴆ�R���I���̗́A���S�͂Ȃǁj�������l�Ɋώ@����邱�Ƃł��B
�@���������āA�n���ɌŒ肳�ꂽ���W�n����ϑ��������̂ɑ��ē����͂ɔ�r���āA�����͂����ΓI�ɖ����ł���قlje�����������ꍇ�ɂ́A�j���[�g���̉^����������Navier-Stokes��������X�I�Ɏg�p���Ă��ߎ��I�A���p�I�ɏ\���M���ł����ł��傤�B
�@��̓I�ɂ͎����������퐶���Œ��ڎ����̖ڂŊώ@���邱�Ƃ̂ł���悤�ȋ�ԓI�E���ԓI�ȋK�͂̉^���ł���A�n���ɌŒ肵�����W�n�ŋL�q�����^���ɑ��Ă��ߎ��I�Ƀj���[�g���̉^�������������藧�ƍl���č����x������܂���B
�@�Ƃ��낪�A�ΏۂƂ���^���̋�ԓI�A���ԓI�ȃX�P�[�����傫���Ȃ�Ǝ���Ɍ덷���傫���Ȃ�܂��B�����ȗ�ł����A�������C�e�̋O���v�Z�ł́A�P���Ƀj���[�g���̉^����������K�p���邱�Ƃ͍���ł��B�C�e���͎̂��_�ƍl���Ă������x���Ȃ��ł��傤���A�C�e�̔��ċ����������Ȃ�Ɣ��˂ƒ��e�̎��ԍ��ƒn���̎��]�^���̉e���ł��������C�e�ɐi�s�����ɑ��Ē��p�̕�������͂��ċO�����Ȃ����Ă���悤�ȉ^���Ƃ��Ċώ@����܂��B���́u�������̗́v���R���I���̗͂��邢�͓]���͂ƌĂ�銵���͂ł��B
�@���_�Ƃ݂Ȃ���C�e�̋O���v�Z�̂悤�ȒP���ȉ^���̏ꍇ�ɂ́A�j���[�g���̉^���������������͂����݂̗͂̂悤�ɂ�������g�ݍ������Ƃɂ���ĖC�e�̉^����\�����Ƃ��ł��܂��B
�@�������A���̂̉^���ł͖�肪���G�ɂȂ�܂��B���̂͑̐ς������Ȃ����z�̎��_�ł͂Ȃ��A�L���̑̐ς����A���̂ł���A�l�X�ȑ����������Ă��܂��B�������j���[�g���̉^���������͗͂Ǝ��_�̉^���ȊO�̑��������ׂĎ̏ۂ��邱�Ƃœ�����Ă��܂��B�j���[�g���̉^���������ł���킳���^���͉t�I�Ȍ����ł��B
�@Navier-Stokes�������́A�S�����̂Ƃ����A���̂̒��Ɂu���̗��q�v�Ƃ����ώ��ň�̖��x�A�S������`�ł�����x�̔����Ȓ����̂����肵�āA�S�����̂��\�����镪�q�̎��̂��̏ۂ��������ŁA�j���[�g���̎��_�ɑ���^���������Ă͂߂邱�Ƃɂ���ē�����Ă��܂��B
�@���������ۂɂ́A���̗��q�Ƃ͑����̕��q�̏W���̂ł��B���̗��q�͂����^�����邾���̎��_�Ƃ͈قȂ�A���̒��ł͔M�͊w���ہA���w���ہA�d�����ۂȂǂ̕������w�ω������݂��A���̂Ƃ��Ă̋����͕s�t�I�ł��B����ɗ��̗��q�͋��łȊO�k�ŕ����ꂽ�̈�ł͂Ȃ��A�^������ߒ��Ōn�O�Ƒ��݂ɍ����E�g�U���Ď��X���X�Ƃ��̐������ω����܂��B
�@��C�̉^���ł���A�Ⴆ�Ή��M�����n�\�߂��Ōy���Ȃ�����C�����q�^���������ɂȂ�̐ς��c��������C�́A�P�ɖ��x�̏�������C�Ƃ����O�`�I�Ȍ`�ł���Navier-Stokes�������ɔ��f����܂���B�܂��A�㏸���鎼������C�͌����ɂ��̐ϖc���ɂ�鉷�x�ቺ�ɂ���ĘI�_�ɒB����Ɛ����C���Ì�����Ƃ������ω����N����A�̐ρE�C���ω��������A�Ì��M���邱�ƂɂȂ�܂��B�ԊO�����C�̂��܂ދC�͓̂d�����ۂɂ���ē����G�l���M�[���ω����܂��B
�@Navier-Stokes�������ɂ͗z�Ȍ`�ŕ\��Ȃ������̗��̗��q�ɓ���ꂽ�������w���ۂɂ�鉷�x���͂��߂Ƃ����ԗʂ̕ω��͗��̗��q�̉^���ɂ������S���▧�x�Ȃǂ����ɕω��������̂̉^����ω������܂��B
�@�������A���̗��q�̉^���ɒ��ڂ������̂Ȃ����ۂ₻��ɂ�����镨���ʂ��̏ۂ��邱�Ƃɂ���č\������Ă���Navier-Stokes�������ł͗��̗��q�̓����ŋN���镨�����w���ۂf���邱�Ƃ͂ł��܂���B���̗��Ԃ��Ƃ��āANavier-Stokes���������瓾��ꂽ���̂̉^����Ԃ���A���̗��q�̒��ŋN�����Ă���l�X�ȕ������w���ۂɑ��č����I�������̂Ȃ���Ԃ���ӓI�Ɍ��肷�邱�Ƃ͕s�\�ł��B
�@���ʈȊO�Ɍ��������Ȃ����_�Ƃ������z�̕��̂ɑ���͂Ɖ^���ɂ��Ă̊W���L�q�����t�I�ȃj���[�g���̉^���������̃A�i���W�[�Ƃ��āA�L���̑̐ς������A����镨���ɋN����l�X�ȕ������w���ۂɂ��ω����A�ό`�E�������Ȃ���^�����闬�̗��q�̕s�t�I�^���Ɋg�������Ƃ���ɖ{���I�ȍ����̌���������̂ł��B
�@�@���������āANavier-Stokes�������́A�����͂̉e���������ł�����x�̋�ԓI�A���ԓI�ȃX�P�[���ŁA���������̓��ŋN���镨�����w���ۂ�����ɑ��đ傫�ȉe����^���Ȃ��ꍇ�Ɍ����ēK�p���邱�Ƃ��ł����ƍl�����܂��B
�@�n���K�͂̋C�ی��ۂ̊�b�ƂȂ��C�̉^���́A�����͂̉e�����傫���A��C�̉��x�A���x�A�d�����ۂȂǂ̉e���������邽�߁A��ʓI�ɂ�Navier-Stokes�������̓K�p�͈͂���ƍl�����܂��B
2.�@Navier-Stokes�������̐��l��͂ɔ������
�@1.�ŏq�ׂ��Ƃ���A���������S�n���K�͂��邢�͓��{�̋C�ۗ\��Ɏg�p����V�C�}�͈̔͂��J�o�[����悤�ȑ��I�ȋC�ی��ۂɑ��āANavier-Stokes�������Ɋ�b��u�����l�V�~�����[�V������p���邱�Ƃ͓K�p�͈͂��Ă��܂��B
�@����ł��u������̋C�ۗ\�����x�͂����Ԃ�オ�����ł͂Ȃ����I�v�Ƃ������_���������Ă������ł��B�������A�u��T�Ԑ�̗\�I�����邱�Ƃ͂قƂ�ǂȂ��v�Ƃ����̂������ł��B
�@���̓_�ɂ��ẮA�O��̒��{����̉���ɂ������w�f�[�^�E�A�V�~���[�V�����iAssimilation,���f���̒l���f�[�^�ɓ�������j�x�ɂ���Ď�������Ă��邱�Ƃł���A����͐��l�v�Z���ʂ����ۂ̊ϑ��l�Œu��������Ƃ����J���j���O�s�ׂ��s���Ă��邩��ł���A�{���̃V�~�����[�V�����Z�p�̌���Ƃ͂������Ȃ��ƍl�����܂��B
�@�b�����ɖ߂��܂��B���ݑ��I�ȋC�ۃV�~�����[�V�����ŗp�������C�̗̈敪�������Ă����܂��傤�B�����w��������2015�N�̃��|�[�g������p���Ă����܂��B
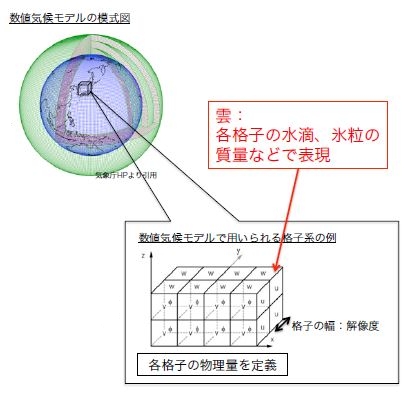
�@����10�N�ԂŊi�q������100km���琔100m�Ɂu���𑜓x���v�����ƌ֎����Ă��܂��B�������A��100m�̊i�q�̒��Ɋ܂܂���Ԃ�Navier-Stokes�������̑ΏۂƂ��Ă��闬�̗��q�Ƃ͔�ו��ɂȂ�Ȃ�����ȑ̐ςł���A���̒��Ɋ܂܂���C�̉^���̐�����i�q�_�̃p�����[�^������p���ēK�ɕ\�����ƂȂǑS���s�\�ł��B����ł́A���Ƃ�Navier-Stokes�����������̗��q�̉^���𐳂����\���ł���Ƃ��Ă��A���l���f�����̒i�K�ł܂������䖳���ɂȂ��Ă��܂����Ƃ͓��R�ł��B���݂̋C�ۃV�~�����[�V�������l���f���͎q�����܂��̃R���s���[�^�[�Q�[���Ƃ����Ă��d�����Ȃ��ł��傤�B
�@���āA���͂܂��܂�����܂��BNavier-Stokes�������ɂ���ē���ꂽ����̐��瓾�������ł́A�i�q�̈�����ŋN�����Ă���l�X�ȕ������w���ۂ����m�m�R�g�����Ƃ��Ĉ�ӓI�Ɍ��肷�邱�Ƃ͂ł��܂���B�܂��O�q�̒ʂ�A�i�q�̈�̋���ȋ�ԓ��̕������w���ۂ��i�q�_�p�����[�^�����œK�ɐ������邱�Ƃ͕s�\�ł��B
�@���������āANavier-Stokes�������ɂ���ē���ꂽ����̐���ƋC�ی��ۂŏd�v�ȏ��ł��鉷�x�A���x�A�~�J�ʂȂǂ̒l���֘A�t���邽�߂ɁA�����̃��m�m�R�g�����ł͂Ȃ��u�d�|���v���v���O�����v�҂����ӓI�ɑg�ݍ��ޕK�v������܂��B���������āA�C�ۃV�~�����[�V�����͌����̋C�ی��ۂ̕����i���m�m�R�g�����j��͕킵�Ă���̂ł͂Ȃ��A�v���O�����v�҂ɂ���č��ꂽ���\�̐��E���R���s���[�^�[�Q�[���ɂ����Ȃ��̂ł��B
�@���Ɏ��ԕ����̃X�P�[���̖��ł��B��ʓI�Ȕ���E����`�Ȍ��ۂ�ΏۂƂ������Ԕ��W�^�̐��l�V�~�����[�V�����ł́A���ԕ����ɕω����ׂ����������Č��ۂ�ǐՂ��邱�Ƃ��K�v�ɂȂ�܂��B���ۂ̎��ԕω��ɑ��ēK�Ȏ��ԊԊu�ŒǐՂ��Ȃ���Α傫�Ȍ덷�����邱�ƂɂȂ�܂��B
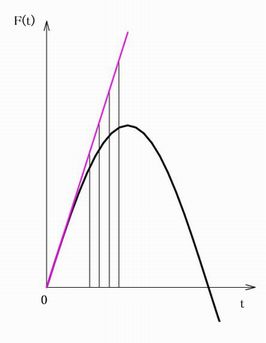
�@�Ⴆ�A���̎����Ŏ������Ȑ������ԒǐՂ��镨������F(t)�̐������Ƃ��܂��B���A����t=0�ɂ����āAF(0)�Ƃ��̎��ԕω���dF(0)/dt���ϑ����邱�Ƃ��ł���Ƃ��܂��B���ۂ�F(t)�̐����͕�����܂���AF(0)��dF(0)/dt���g���āA���ۂ����f���������v���O�����ŏ����\�����s���܂��B�}�ł͐��`���ŏ����\�����s���Ă��܂��B
�@���āA�}���番����悤�ɁA��ʓI�Ɋϑ��l�����݂��鎞������\�����鎞���̊Ԋu���傫���Ȃ�ɂ��������āA�����Ɨ\���l�̘������傫���Ȃ�܂��B�����ŁA�Ȃ�ׂ��Z�����ԊԊu�ŏ����\�����s���܂��B���̌��ʂ��瓾��ꂽ�����ʂŐ��l���f���̃p�����[�^���C�����čX�ɏ����\�����s���܂��B������J��Ԃ����ƂŒ����Ԃ̏����\�����s�����ƂɂȂ�܂��B
�@�������A���Ƃ����l���f�������ۂ̕������ۂ𐳂����͕킵�Ă����Ƃ��Ă��A���F�A���l��͂Ƃ͉�͉��������Ȃ����ɑ��Đ��l�I�ɋߎ��������߂邱�Ƃł���A�J��Ԃ��v�Z�̑����ɂ���Č덷���~�ς��A����Ɍ����Ƃ̘����͊g�債�Ă����܂��B�C�ۗ\�����l���f���̂悤�Ȍ��׃��f���ł́A���꒷���Ԃ̏����\���ɂ͑ς����܂���B
�@����A���Ƃ��o���̈������l���f���ł��낤�ƁA���ۂ̊ϑ��l�Ńp�����[�^���C���i�w�f�[�^�E�A�V�~���[�V�����iAssimilation,���f���̒l���f�[�^�ɓ�������j�x�j��������̒Z���Ԃ͎��ۂ̌��ۂƂ̘����͏������A�������㐸�x�̍��������\�����ł��܂��B���������āA���X�o���̈������l���f���ł����Ă��Z���Ԃ̋C�ۗ\��A��̓I�ɂ͂Q�C�R�����x�̗\��ł���Έ�ʑ�O������E�����Ȃ����x�̐��x�i�j�̗\���͂ł����̂ł��B�������A��T�Ԑ�̓V�C�\���M����l�͂قƂ�ǂ��Ȃ��̂������ł��B
�@���āA�C�ې��l�V�~�����[�V�����Łu�ߋ��̋C�ی��ۂ��Č��ł����v�Ƃ������Ƃ��悭�����܂����A���ۂɂ͂��܂��Č��ł��Ă��邩�ǂ����������邱�Ƃ����s�\�Ȃ̂ł��B�ߋ��̋C�ۂ̏�ԂƂ��ăf�[�^�����݂���̂͒n���\�ʂ̌���ꂽ�C�ۊϑ��_�̃f�[�^�ɂ����܂���B�C�ۗ\�����f���͑Η�����C��ΏۂƂ��ă��f�������Ă��܂��B���������āA�n�\�ʂ����ł͂Ȃ��Η�����C�̂�����Ƃ���Ō�����C�̊ϑ����ʂ�K�ɕ\���ł��Ă�����������邱�Ƃ��V�~�����[�V�������������Ɣ��f���邽�߂̕K�v�����ł����A�����ɂ͔�r�ΏƂ��ׂ��ϑ��l�͑��݂��Ȃ��̂ŁA���̐��x�������邱�Ƃ͕s�\�Ȃ̂ł��B�p�����[�^���������Ēn�\�ʂ̊ϑ��f�[�^�̍Č������Ɍ����������Ă��A���l���f���̉��ǂƂ͖����Ȏ��Ȗ����ɂ����Ȃ��̂ł��B
�@���݂̋C�ۗ\���V�~�����[�V�����ł́A�O��̒��{����̉���ɂ���ʂ�w���݂̂��ׂĂ�IPCC���f���̌��ʂ́A��w��C�̉��x�V�~�����[�V�������ϑ��ɍ����܂���B�@IPCC�����J���Ă���C���̉����f�ʐ}�ŁA�M�я�������ƁA������܂����A�M�я��Ŋϑ����ʂƃ��f�����ʂ��S���قȂ�܂��B�x�Ƃ����̂������Ȃ̂ł��B
�@��N�Ă̋�B�k�����J�ɂ��āANHK�X�y�V�����u�ُ�C�ہE�X�[�p�[�䕗�v�Ƃ����ԑg������܂����B���̔ԑg�ɓo�ꂵ�����É���w�ؘ̒ؖa�v���i�n�����z�����Z���^�[�C�ۊw�������j�́A�u���{�̍ŐV�s�̍����x�̋C�ۗ\�f���ɂ��V�~�����[�V�����ł�����B�k�����J��\�����邱�Ƃ��ł��Ȃ������B���g���ɂ��ُ�C�ۂ͂���قǂ܂łɈُ�ɂȂ��Ă��Ă���B�v�Ƃ�����|�̔��������Ă��܂����B����͐��ɕ��т��̂Ƃ����ׂ��R�����g�ł��B
�@�����ɋN�����Ă���C�ی��ۂ́A���ꂪ�ϑ��j�㏉�߂Ă̋H�L�Ȍ��ۂł��낤�ƁA���R�̂��Ƃł���100�������I�Ɂi���m�m�R�g�����Ƃ��āj���������ۂł��B�ނ̃R�����g���u���{�̍ŐV�s�̍����x�̋C�ۗ\�f���ɂ��V�~�����[�V�����́A�ق�̔�����̏W�����J�Ƃ�������ȋC�ی��ۂł����܂Ƃ��ɍČ����邱�Ƃ��ł��Ȃ������B�v���Ƃ��������Ă���̂ł���A���S�Ȕs�k�錾�ł����B
�@�܂�A���݂̍Ő�[�̐��l�v�Z�Z�p�̐������W�����C�ۗ\��V�~�����[�V�����ł��A��B�k���n����x�͈̔͂ŋN���錃��ȋC�ی��ۂɂ��ẮA2�A3���ǂ��납������̗\��ł��S�����ɗ����Ȃ����Ƃ������ɂ���Č����ꂽ�Ƃ������ƂȂ̂ł��B
No.1243 (2018/11/09) ���̗͊w�V�~�����[�V�����̓K�p���E���l����B
���̗͊w�������ɂ��Ă̑f�p�ȋ^��
�@��x�ɂ킽���āA���{����N����̗��̗͊w�������Ɋւ���_���̓��e�ɂ��ĕ��Ă��܂����B�����g�͓y�̍\�����Ȃ̂ŁA�\������e�Y���A���̂̉��͉�͂Ŕ����������̐��l��͂ɂ����闣�U���̎�@��A���l�v�Z���o�����Ă��邾���ŁA���̂ɑ��鐔�l��͂ڌo�����Ă���킯�ł͂���܂���B���̗͊w�������ANavier–Stokes�������ɂ��ẮA�y�؉Ȃ̉Ȗڂ̈�Ƃ��Ċw�����w�ɂ����āA��{�I�ȍl����������������炢�ł��B
�@���̂悤�Ȃ킯�ŁA�ǂ����Ă����͉��͉�͂̃A�i���W�[�Ƃ��ė������悤�Ƃ��Ă��܂��܂��B���͉�͂ł͘A���̂̕����̕s�A���ɕω�����_�A���邢�͂Ђъ���Ȃǂ����݂���ƁA���͏�͊��炩�Ȋ��ŕ\���ł��Ȃ����߂ɁA�v��ʑ傫�Ȍ덷���邱�ƂɂȂ�܂��B����ł����͉�͂Ƃ��������i���Ԍo�߂ɑ��ĕω����Ȃ����j�����߂���ł���A�\�ߓ��ِ��̂�����邱�Ƃ��\�������ꏊ�ɑ��ē��ʂ̗̈敪����d�|����g�ݍ��ނ��Ƃő傫�Ȍ덷��������邱�Ƃ��ł��܂��B
�@�����������̌o������́A�n���S�̂��J�o�[���鋐��ȃX�P�[���ŋN����C�ی��ۂƂ�������Ȗ��\�\������Ƃ���ɕs�A���ʂ���ٓ_�����I�ɔ����E���ŁE�ړ����J��Ԃ��悤�Ȗ��\�\�ɑ��āA�����ȗ��̗��q�̋����ɂ��ċL�q��������`�Δ�����������p�������l�v�Z�œK�Ɏ��Ԕ��W�I�ȋ������Ԃɂ킽���ĒǐՂ���ȂǂƂ������z�́A�u�r�����m�v�Ƃ����`�e���������Ǝv���Ă��܂��B
�@���̂悤�Ȃ킯�ŁA���̗͊w�������ɂ��đf�l�̎��������f�p�ȋ^��ɂ��āA���{����Ƃ̃��[���̂����ŁA�����ł�������[�߂悤�ƍl���Ă��܂��B���{���狖���������������[���ɂ��āA�������̃R�[�i�[�ŏЉ�Ă��������Ǝv���܂��B�܂��A�^���ӌ��̂�����͂��A������������A����������Ă��������ƍl���Ă��܂��B�����5���ڂɂ��ĉ����������܂����̂ŁA�ȉ��ɏЉ�܂��B
��P�F�i�r�G�X�g�[�N�X�̕������́A�S�����̂ɑ���j���[�g���̉^���������ł���Ɨ������Ă悢���H
��
�@�͂��A�����ł��B
�@�i�r�G��X�g�[�N�X�������Ă�������̓j���g���͊w�̑S�����ŁA������ϑ����ۂ�
�i����m�jX(�����xa�j���q��F�r
�Ō��肷����@�i�����ł��v�f�ɊҌ����āA�v�f�̋O�Ղ�F=ma�ŏ������������{���V�s�̕��@�j�����s���Ă����̂ł��B
�@�����̊ዾ��������ƁA��X�́uF=ma�A���Ȃ킿��F�����̗��q���^��������v�Ƃ����ʂ��G�ɕ`���܂��B���ꂪ�����̔F���@�ł��B�Ƃ��낪�A�d���C�w�̐��w��ʎq�͊w�́A�͂��߂͊ϑ��Ώۂ̌��ۋL�q����n�܂����̂ł����A�������u�ϑ��Ώۂɂ͂��炭�͂������ł��̌��ʊϑ��Ώۂ̈ʒu���ړ�����v�Ƃ������Ռ���̌`���ł͂Ȃ��A�u���Ԃ̊e�ꏊ�ɗ͂̑f�����ߍ��܂�Ă���v�Ƃ���`����̎v�z�ɐ��߂��܂ꂽ�̂��Ǝ��͎v���܂��B���ꂪ�u��̎v�z�v�ł��B�}�b�N�X�E�G���������͓d�����\������A�������������ł��B�}�N�X�E�G���͂��̓d����̕�������������ɂ�������炸�A�u����ł��i�j���[�g���搶���������悤�Ɂj�͂��d�ɂ⎥�ɂɓ����Ă���̂��v�Ǝv���������������ł��i�ǂ����œǂ̂ł����A�ǂ̖{���͂����������܂���B���������w��3�N���Ŏ����̗͊w�̐��w���}�b�N�X�E�G���̓d���C�w�̐��w�Ƒ�ςɂ悭���Ă������Ƃɕs�v�c�Ɏ䂫����ꂽ���Ƃ����v�������܂��B�j�ȉ��̉���ɂ������܂����A�j���[�g���͊w�ŋL�q���鎿�_�̗͊w�̓|�A���J���̈ʑ���ԂŗL�������̋O�Ղł����A�d�����ʎq��͈ʑ���Ԃł͂Ȃ��q���x���g��ԂŖ��������̋O�Ղ̂͂��ł��B�܂�A�j���[�g���͊w�͊ϑ��Ώۂ̓����\���ɂ͓��ݍ��܂��ɁA�L�����̊ϑ��Ώۂ̏�ԁi�ʒu�Ƒ��x�j���Ɍ��肷�鎞��̊w�ł��B�������A�d���C�w��ʎq�͊w�͖������̏�̗ʂ��A���łɋ�Ԃɔ�����Ă���悤�ɕ\������Ă��܂��B
����F
�@�i�r�G�X�g�[�N�X�������̐��w����̍\���́A��X�̔F������点��ޗ������ڂ���Ă��܂��B���ڂ��ꂽ���w����̍\���Ƃ����̂́A�u�ϑ����ꂽ���ۂ��܂��L�q���A���̎��ɉ�X�����ɍ�肠����ϑ��Ώۂ̎ʂ��G�Ռ���ŕ\�����邽�ߔ����������̂��Ƃł��B�{���́A���ՓI�Ȑ��w����������Ŏg���āi�������������āj�݂�A�ȒP�Ɏ������₷���̂ł����B�����ł͊Ȍ��ɉ�X�̔F������点��f�������v�����܂܂ɗ��܂��B
����̑f�@�F
�@�O�ҁi�ϑ����ۂ̋L�q�̒i�K�j�ł͌o�����瓾��ꂽ�A�[�I�Ȗ@���ŁA��҂͕��ՓI�Ȑ��w����ʼn�X�̓��ɏ����ꂽ�ʂ��G�̉�㈓I�Ȗ@���ł��B�����͌�҂��@���ƌĂԂ��Ƃ�����܂����A���ꂪ�댯�̑f�ł��B�Ⴆ�A�O�҂͎��_�̎��ʂƉ����x�̐ς����_�ɓ����O�͂ɓ������ƌ����A�����i����ꂪ�ϑ����錻�ۂ̃R�g�����j�ł����A��҂̓i�r�G�X�g�[�N�X�̔����������Ƃ������w�����p���āA�����x�C�R�[���͂Ƃ����`���ŕ\������Ă��邩��ŁA��������ƃi�r�G�X�g�[�N�X�������̍��ӂ̔���`�������ʂ������̗��q�̉����x�i���������x�j���͊w�n���_(Dynamical
System) �ŏd�v�Ȗ������ʂ������ƂɋC�����Ȃ��댯������̂ł��B
����̑f�A�F
�@��X���ϑ����Ă��闬�̂�C�̂Ȃǂ̘A���́i�L���̐ς����ϑ��Ώۂ��ό`���Ȃ��j�́A�O�����ƔM�╨�����������邩��A�ϑ��Ώۂ̎��ʂ͎��ԂƋ�ԂɈˑ����܂��B�Ƃ��낪�A�i�r�G�X�g�[�N�X���������i�I�C���[���������j�ϑ��Ώۂ̎��ʂ����ԋ�Ԃŕω�������L�q���̂Ăāi�p�����āj���܂��i����A�̂Ă�ƌ������́A�u�L���̑傫���̗��q���̂Ȃǂ͑��݂��Ȃ��H��v���ƉR���Ė��E���Ă���Ƃ����ق���������₷���j�B���̂��Ƃ��킽���́u���̗��q�̖��x�𑼏����炱�����薧�A���Ă���v�ƕ\���������Ƃ�����܂��j�B���̂��Ƃ̓j���[�g���͊w�ŕ\������ÓT�͊w�n���_�ł͑�ςɏd�v�ł��B
����̑f�B�F
�@���ۂ̋L�q�̒i�K�ł́A���ʂƗ���̈ڗ���(x,y,z,t)u
��u/��x�ł������̂ɁA���̍��̓i�r�G�X�g�[�N�X�������ł͗���̔���`��u��u/��x�ŕ\������A��������Ύ��ԂƐ��ԍ��W�ŏ�����Ă��܂��B����Ȑ��w�ዾ�����������Ă���ƁA�u����̋����̐����i����`�j�Ɨ���镨�̂̐����i���x�����L���̑傫���̗��q�j�Ǝ�����W�̑��ݍ�p�v�����������Ƃ�����܂��B�i���̂��Ƃ̓x�i�[���Η����ۂ��J�I�X�̕������̌`�ɕ\�����Ă݂�A��t/��,
��T��t/�ȃ�,
�Ȃǎ��ԍ��W�Ɨ��̂̐��������ɂȂ��Č���邱�Ƃ��番����܂��j�B�ϑ��Ώۂ̌��ہi�̕����j�ɖ��ڒ��ɂȂ�Ɓu�R���s���[�^�[�R�[�h���^�]����Ζ������\���ł���悤�ȋC�ɂȂ�܂��B
����̑f�C�F
�@�i�r�G�X�g�[�N�X�������Ɍ�������`���ƔS���̂�����������Ō��߂���@�͊m�����Ă���̂ł����A�������߂�����`�p�����[�^�ƔS���p�����[�^�̑傫����`�̔����ȍ��ɂ���āA����̕��U���ƎU�퐫�̂����ꂪ�������邩���A�i�r�G�X�g�[�N�X�������͌���ł��܂���B�i������₷����́A�O�҂̓\���g���g�����������A��҂͗��������������邱�Ƃł��j�B
����̑f�D�F�@
�@���ԉt�̃j���[�g���̗͊w�𗬑̗��q�ɂ��Ă͂߂Ȃ���A�M�̕�����d�C���C������ʎq�������A�i�r�G�X�g�[�N�X��������2�̃p�����[�^�i���x�ƔS���j�̉A�ɉB�������߂ɁA�i�r�G�X�g�[�N�X�������́A���ԉt���i��Ύ��ԂƐ��Ԃ̔��]�Ώ̐��j�Ǝ��ԕs�t��������g�݁A���̌��ʃi�r�G�X�g�[�N�X�������̐��w�\���͊��S��2�̌��ۘ_�I�p�����[�^�Ɋ��S�Ɏx�z���ꂽ�̂ł��B���̂��߂Ƀi�r�G�X�g�[�N�X�������̉�͊w�I�����i������̉��̑�搫�ƁA��ӓI���݂̖��j�͖������ł��B���̂��߂ɔ����������̊w�I�����i�J�^�X�g���t���_��|�A���J���ȗ��̗͊w�n���_�j�����s���Ă��܂������A����ł��i�r�G�X�g�[�N�X���̗��̗͊w�n�̔����������͑��������āA������ʑ��}��̗����������ɂ�����g��ł��܂��܂��B������t���N�^���̏o���ŁA�܂��܂��D���ł��B�����Ō����u���̑�搫�Ƃ́u�ʑ���Ԃŕ`�������̗����̑S���ɂ킽���āv�Ƃ����Ӗ��ł��B
�@�i�r�G�X�g�[�N�X�������𒆐S�ɐ��������̗͊w�n�̘A������������̌����͂ǂ��ɂ���̂��H�\�\�u��X�̊ϑ����錻�ہi�����j������ꂪ���w�I���Ռ���ŏ����������Ƃ��Ɏ��������m�i�����j�͉����H�v���l���鎞���ł͂Ȃ����Ǝ��͂������܂��B
�Q�l�����́A
���W�[���X�J���F�k�S�����̂̐��w�I���_�A�Y�Ɛ}��1979
Tim Poston and Ian Stewart, Catastrophe Theory and its Applications,
PITMAN, 1978
�t�^�P�F
�@�j���[�g���͊wF=ma�͎��ԉt�ł����A�i�r�G�X�g�[�N�X�������͋����I�ȗ��̗��q�i�傫���������A�������ׂ̗��q�Ǝ��ԕs�t�ȔM�I�E�����I�ȑ�������p�����Ă���A���ꂪ�������������������̊ዾ�j��Ώۂɂ������ԕs�t�̐��w�\���ɏ�����Ă��܂��B�������A���ۘ_�I�ȃp�����[�^�ɑ�ςɕq���ȍ\���i�s����\���j�ł��B�\������Ƃ������t�͂��łɃJ�^�X�g���t���_�Ŏg���Ă��܂����B
�@�����ʼn�X�́u���̃R�g�����i�����j�v���������݂܂��B���̗��q�̒��S�̈ʒu�Ƒ��x���u�ԓI�Ɍ��߂邾���Ȃ�A�j���[�g���͊w�̔��������������������̂ł����L�����Ԍo�߂���ƁA���̖��x�����ω����܂��B�܂��A���̗��q�͑傫�������̂ŁA�����I�ړx�ł��ׂ̗��̗��q�Ɨ͊w�I���ݍ�p���s�Ȃ������łȂ��A�~�N���i�d�C�I�A���w�I�A�ʎq�͊w�I�j�ړx�̑��ݍ�p������܂��B�Ƃ��낪�i�r�G�X�g�[�N�X�̎��͂��������ׂĂЂ�����߂āA�����I�ȔS���Ƃ������ۘ_�I�ȃp�����[�^�ő�\�����܂��B�܂�A�~�N���ړx�̑����̎��R�x�������̗͊w�n�ł́A�B�ꂽ���ׂẴp�����[�^���w�肷�邱�Ƃ́i�v�Z�������[����̂Łj�s�\�ł�����A�����I�Ȍ��ۘ_�i���ϒl�A���U�A�Ȃǂ�����~�N���ړx�̓��v�ʁj�ő�\������̂ł��B
�t�^2�F�@
�@�j���[�g���͊w�ƑS�����ƂȂ�A�o���I���ۂ��I�ɋL�q������@���J���m�[�A�N���E�W�E�X�A�M�b�u�X�̔M�w�ł��B���q�_���o�ė������ƂŁA�j���[�g���͊w�̎��_�i�_�q�̈ʒu�����肷�鎞�ԉt���@���j�Ő������悤�Ƃ��鎎�݁i���v�͊w�j�Ɍq����܂��B
��1-2�F�����x�n�ł���n���S�̂�ΏۂƂ�����I�ȗ��̉^���V�~�����[�V�����ɑ��āA���������K�p���\�Ȃ̂��H
��
�@�ۂł��B
�u���I�ȗ��̉^���v�Ƃ́u�_��̗��q���A�n���ړx�̋������ړ����邱�Ƃ��v�Ɖ��߂���l�i�Ⴆ�A��O�̋C�ۊw�҂���t����I���S���܂Ŕ�������D���e�̋O���\�����������{�̋C�ۊw�ҁj�ɂƂ��Ă͎��p��͉\�������̂�������܂���B�������A����}�X���f�A�̕L�҂ɑ��ĕ����@�����g�����C�g���V�~�����[�V�����R�[�h�Œn���̏����̋C���\������ȂǂƎɊ|���A�ߋ�100�N��������̒n��C���̏㏸�͉��ΔR���̔R�ĂɌ���������ƌ��_����ړI�����̂��߂Ɂu���I�V�~�����[�V�����v�̓���Ɏg�����Ƃɂ͎��͓��ӂ������܂���B
�@���̎�̎̓���͎��ԉt�̃j���[�g���͊w�Ǝ��ԕs�t�̔M�͊w�ӓI�ɍ������킹�Ă���ƌ����Ӗ��ŗ͊w�n�̗��_�̌����ɂ͑傫�ȕ��Q������ڂ��܂��B
�@�����ȗ͊w�n���_�̎Q�l������
Gerald looss and Daniel D. Joseph: Undergraduate Texts in
Mathematics., Elementary Stability and Bifurcation Theory, Springer
ISBN 0-387-97068-1
��2�F�i�r�G�X�g�[�N�X�̕������ŋ��߂�����̏�ԂƁA���̂̉��x�̊W�͂ǂ̂悤�Ɋ֘A�t����̂��H
��
�@���ꂪ�A�u�����͗��̗͊w�Ƃǂ��t���������H�v�ɏ������@�A�A�A�B�ŁA���݂̗��̗͊w�n�̕������̒v���I���ׂł��B
�@���݂̊C�m�z���f���ł��A�C�m��z���f���ł��A��C�̑�z���f���ł��A�����Ə������ړx�̊C�m���C���f���ł��A�u�i�r�G�X�g�[�N�X�������͉��x�𖧗A���A���x�g�U�������͗���x�N�g���𖧗A�v���Ă��Ă��܂��B����JAMSTEC�ŋ��Ȋw�Z�p���̍��Y�C�m��z���f���\�z�v����Ă����Ƃ��i1992�N�j�ɁA���̂��Ƃ��C�ɂȂ�܂����B�܂��A2007�N�ɗ�����w�ŊJ���ꂽ���{�C�m�w��ŁA���̖���₤�V���|�W�E����������Ă��A��1�l�ŊJ�Â����̂ł����A���̃V���|�W�E�����₩���ĎQ�����Ă��ꂽ�C�m�w�҂͐��l�i���l���̃��f�����o���������Ƃ��Ȃ��悤�Ȑl��3
�l���������H�j�ł����B�܂�A�E�ƉȊw�҂����́A�i�O��̎��́u��X�͗��̗͊w�Ɣ@���ɂ��������H�v�ɇ@�A�A�A�B�Ƃ��ċ������j�A�������������Ԃ̖��A�j�i�A���������������m�ł��݂��ɗ����Ɖ��x���u���A�������Ă��邱�ƂɁA���������C�ɂȂ�Ȃ��̂ł��傤���B�����ł��J��Ԃ��܂����A�͊w�n���_���������鐔�w�҂����͎��ԉt�̃j���[�g���̗͊w�Ǝ��ԉt�̔M�w�������ȒP�ɘA����������͂��Ă��܂���B
��3�F���l��͂ɂ����āA���̔��W������`�ł��Ȃ��s�A���ʂ���ٓ_���܂ޗ̈�͂ǂ̂悤����������̂��H
��
�@�����炭�A���̂��Ƃ́A��s�@�̗��̎���̉Q�̔�����A����̑����Ƃ���łł���Q��A�܂�������A�䕗�̒��̗���Ȃǂ��A�E�ƉȊw�҂������ǂ������A�ǂ��������Ă���̂������Ă���̂��Ǝ��͑z���������܂��B
�@1980�N����1990�N�܂Ŏ����t���������l�X����A���͂����ȍl�����ɐڐG���āA�w��ł��܂������A�܂����̌��_�́A�u�i�r�G�X�g�N�X�������i�̐��i�j�͋ߎ����ł��B�����i�r�G�X�g�N�X�������̗\���������̌��ۂɍ���Ȃ��ꍇ�́A�����̌��ۂ��i�r�G�X�g�[�N�X���̐��w����`���ɛƂߍ��ޗ����i�����I�����܂��́A���I�ł����̏ꂵ�̂��̗����j�����Ē��ԓ������Ŏ��Ȗ������܂��B���ԈȊO�ɂ͂����̔閧�́q�u����Ȃ�����́r�킴�킴���J�͂��܂���B�������A�E�ƉȊw�҂��������̌���������Ė������Ă���Ԃ́A���̗͊w�͂��܂ł����Ă������ƂɌ����������˂����p�����w�҂̏�������ł����Ȃ��Ǝ��͎v���܂��B����JSAMSTEC�ɂ�������ɁA�f�J���g�����i�H�j�̒��p�̍��W���g�킸�ɁA�����x���W�n�i���������̖��x�ʂ����W�ɍ̗p�������w�Z�@�j���J�����Ă��܂������A�����͓��{�ł͎��������g���Ă������̋Z�@�i�����x���W�j�̗L�����ƌ��E���t�̓d�͒�����������_�ސ�̓����X�[�p�[�R���s���[�^�H��x�Ђŏ��ҍu�����A�܂����̋Z�@�̏ڍׂ����Ȋw�Z�p���̍��x���v�Z�Ȋw�����@�\�̎G����Ō��J����L���������܂����B
��3�|2�F�t�̂�C�̂̉^�����ۂɐ�����s�A���ʁA���ٓ_�͎��X���X�Ƃ��̈ʒu���_�C�i�~�b�N�ɕω������邱�ƂɂȂ�Ǝv���܂����A�ǂ̂悤�ɏ�������̂ł��傤���H
��
�@���͋C�ۃ��f�����^�]�����o��������܂��AJSMSTEC�ł̎��̌o���ɂ��Ƃ����ƁA���f�����^�]�������ʁA�����ړI�ȊO�̌��ʂ��łĂ�����A�u����̓��f���̃p�����[�^�̑傫�����������߂��v�ƌ��߂��āA�������ʂ������d�|�����v�Z�R�[�h�Ɏd�g�݂܂��B���̂悤�Ƀ��f����M�邱�Ƃ͋ƊE�p��ł̓��f�������˂��Ď������i�i�b�W���O�j�⓯���i�A�V�~���[�g�ƃJ�^�J�i���t�ŌĂׂΎ��Ȃ̍߈ӎ���Y��܂��j�ȂǂƌĂ�܂��B���̂悤�ȏ��H�́A�iIPCC���̎�M�����Ă���}�C�P���E�}��������������悤�Ȋϑ��f�[�^��₂̃C���`�L�ł͂Ȃ��A�j���f���̏o�͂��ϑ��f�[�^�ɋ߂Â��悤�ɒ�������Z�@�ŁA1960�N�ォ��C�ۂ�C�m�̐��l���̃V�~�����[�V�����ƊE�Ŏ�����Ă����Z�@�ł��B�������A�ϑ��l�ɍ��킹��Ƃ���������������_�������̎�̋Z�@�́A�����̊C���̕����i���m�S�g�̗����j�����A���ʂ��������̊ϑ��l�ɍ����悤�Ȏd�|���i�Z�@�j�����Ă����̂ł��B���̔��������܂��s���A�_���̐��������邾���łȂ��A���E���̓��Ǝ҂��^�����Ă���邩��A���̋ƊE�ŗL���ɂȂ�܂��B
��3�|3�F�@�s�A���ʂƂȂ�Ⴆ�ΔM�ю����т∟�M�ю����сA���ٓ_�ɂȂ��C�����S�t�߂ł͌������C�ی��ۂ��N����ƍl�����܂����A�����I�ȉ������߂���̂��H
��
�@�����Ƃ��x������������ł��s���ł��邾���ł��B����܂łɎ����C�ۊw�҂����Ƃ̌𗬂œ����m���Ŏ��̊��z�����`���������܂��B�܂��A�u�i�r�G�X�g�[�N�X�̉^���������ƔM�͊w�̃G�l���M�[�ۑ�����A�����������̗͊w�n�̕������́A�w������Η����o�ė����ֈڍs���錻���̌��ۂ�^���ł���ۏ͖����v�Ƃ������Ƃł��B���̂��Ƃ́A�i�r�G�X�g�[�N�X�������̍\���s���萫�ƌĂ�Ă��܂��B
�@�i�r�G�X�g�[�N�X�������𒆐S�ɐ��������̗͊w�n�̈�A�̘A���������ł͌����̌��ۂ�^������ۏ�����܂���B
�@�����ŕ��ՓI�Ȑ��w����̍\���͂��̂܂܂ɂ��Ă����A�����Ɋϑ��ł���l�������A�ϑ��l�ŏC������v�z��O�ꂷ��ƁA�f�[�^�E�A�V�~���[�V�����iAssimilation,���f���̒l���f�[�^�ɓ�������j�Ƃ������ۗ\���̓���ł�������܂��B�f�[�^�E�A�V�~���[�V�����̋Z�p���g���ƁA�����̊ϑ��f�[�^�ɓ�������������Ȃ�A�i�r�G�X�g�[�N�X�������̓����͌����̊ϑ��f�[�^����傫������Ȃ�����A�����̎g�p��ł͉䖝�ł���̂ł��B�������A���̂��Ƃ́A�u�����f�[�^�ɓ��������Ȃ��Ȃ�A�����̓i�r�G�X�g�[�N�X�������̓��������̗͊w�n�̎��Ԕ��W�������͉�������̂��킩��Ȃ��Ŏg���Ă��邩��A���݂��珫����\�����邱�Ƃ͂ł��Ȃ��v�ƋC�ۗ\��̌��ƊE�̉Ȋw�҂��咣���Ă��邱�Ƃ��Ӗ����܂��B
�@�i�r�G�X�g�[�N�X�������ƔM�͊w�������������ĔM�т̑Η��̎d�g�݂̐��w�\�����v�Z���Ď������邱�Ƃ�2010�N���납��A���ꍂ��̋@�B�V�X�e���H�w��5�N���̉��p���wII�̎��ƂƁA���ꍂ���U��1�N���̉��p��͊w�̎��Ƃň����܂����B���̌v�Z�������K����̂ɍœK�Ȃ̂́A�O�H�q�Y�F�@�����������Ɨ͊w�n�̗��_����̂P�V�T�y�[�W����P�W�O�y�[�W�ɓ����Ă��郍�[�����c�������i�₩��̂����̑Η����ۂ̕����̈ꕔ���������o����3���̘A�������������j�ł��B�����5�̋����I�Ȍ��ۘ_�I�p�����[�^�i�n���E�ł̉��x����T�A���̖��x�ρA�S���ˁA�M�c���W�����A�M�`���W���ȁj���g���ċ����I�ȑΗ����ۂ��V�~�����[�V�������闬�̗͊w�n�ł��B���̃��[�����c���̉��̐��i�́A�p�����[�^����T/�i�˃ȁj�̑傫���ɂ���đ傫���ς�邱�Ƃ��ؖ�����Ă��܂��B�܂�A���w�\���ɉB���ꂽ�~�N���̕����Ɏx�z����Č���錻�ۘ_�I�p�����[�^�i���A�ˁA�Ȃƃ�T�j���}�N���Ȍ��ہi�₩��̂����̑w������Η����o�ė����ɂ����錻�ہj�o���̈������������̂ł��B
��4�F���k���̔S�����̂������ꍇ�A���̗��q�̖��x�ρA�S���ˁA���xT�A����P�͑��݂Ɋ֘A���A����������̏�Ԃ���̂ŁA���x�̔���`���������ƂɂȂ邪�A�������̂�����邱�Ƃ��\�Ȃ̂��H
��
�@�����闳����A�[�C�̊C����A�Ռ��g�������ꍇ�ł��ˁB�����̐��l�V�~�����[�V�����͌^�̍\�z������Ă���l�������A�����J�ɂ��܂����A�ǂ̂��炢�������Ă���̂����͂���܂���B�ł��A�f�[�^��₂Ȃǂ̃C���`�L�������Ȃ���A���̏ꂵ�̂��̊Ԃɍ��킹�̕��@�������Ăł��A�������g����Z���Ԃ̋C�ۗ\��̖ړI�ł́A���ۂ̗\�������������ł����̂ł��B�������A�i�r�G�X�g�[�N�X�������̍\�����萫���ؖ��ł��Ȃ�������́A����Ȃ邻�̏ꂵ�̂��̋Z�I�J���ŏI����Ă��܂��Ǝ��͎v���̂ł��B���̂��Ƃ�
FITCH, MARLOW, DEMENTI�@���@CRITIAL�@PROBLEM�@IN�@PHYDICS�@1997�N
��A
YAU���AAsymtotic solutions�gDynamics of Many body Systems and classical
continum Equations
�ɂ�������Ă��܂����B
��5�F�C�ۃV�~�����[�V�����ł́A�C����~�J�ʂ��d�v�ȗv�f�ƂȂ�Ǝv���܂����A��C�^���̃V�~�����[�V�������ʂƑc��̂Ȃ������I�ȊW����`�\�Ȃ̂ł��傤���H
��
�@�C���̉������z�͋�C�̉�ɓ������͂����肵�܂��B�Η����̒���ŁA�ϗ��_�͉J���ɂȂ�A�����C���n�ォ��^��ł����M�G�l���M�[�͑Η�����w�ɂ͂Ȃ���A��w�͉��߂��܂��B
�@���݂̂��ׂĂ�IPCC���f���̌��ʂ́A��w��C�̉��x�V�~�����[�V�������ϑ��ɍ����܂���B�@IPCC�����J���Ă���C���̉����f�ʐ}�ŁA�M�я�������ƁA������܂����A�M�я��Ŋϑ����ʂƃ��f�����ʂ��S���قȂ�܂��BIPCC�Ƃ����e�����{���\����@�ւ����̂悤�Ȑ}�����J���Ă���̂ŁA������������A���̂��Ƃ��C�ɗ��߂Ă��镨���w�҂�C�m�w�҂�C�ۊw�҂���Ƃ�����̂�������܂���B
�@�Ȃ����E�e�����{���\����C�ۊw�҂����͔M�я��̋C���V�~�����[�V�������ԈႦ���̂��H���̗��R��IPCC�ɏW�܂������E�e���̋C�ے����̗p������C���f���̑S�Ă��A�M�т̑Η����ہi�C���A�㏸�C���A�ϗ��_�A�~�J�j��\�����镨���i���m�S�g�̃R�g�����j���R���s���[�^�i���f���j�ɏ�����Ă��Ȃ����Ƃ������ł��B
�@���ۘ_�I�ȃi�r�G�X�g�|�N�X�������𐘂������̗͊w�n�̘A�������������̑Η����ۂ�S�����ۂ̃p�����[�^�������̂ƁA�����������烉�W�[���X�J���̖{�̖�҂����Ƃ����ŏ����Ă���悤�Ƀi�r�G�X�g�[�N�X�������ɍő�̗��_�I��Q���B��Ă���̂�������܂���B����ɂ�������炸�A���̍��̋���V���̑S�ʂԂ������L����A���卑�c�����́u�n���ɂ₳���������W�ԑg�v�ŁA�u�����@���Ɛ��E�ő��̃X�[�p�[�R���s���[�^�ŁA���N��A���\�N��A100�N��̉��g����\������v�Ƃ��̍��̐E�ƉȊw�҂͌����܂��B�e�����{���\����CO2���g�����f�����M�я��ŋC�����z��v���I�ɊԈႦ�Ă����C�ł���̂ɂ�������炸�ł��B
�Q�l�F���W�[���X�J���u�k�S�����̂̐��w�I���_�v�́u���_�v�����Ɓu��҂��Ƃ����v

��҂��Ƃ���

�u��҂��Ƃ����v�Ə��_�ɑ��钆�{����̃R�����g
���킽����
�u�i�r�G�X�g�[�N�X�������̂ǂ�������������炷�̂����l���Ȃ��܂܂ɁA�E�ƉȊw�҂����͂Ȃ���{�X���J�n�����i�r�G�X�g�[�N�X�̗��̌n�\���̌v�Z�R�[�h�����{�b�g�̂悤�ɉ^�]����̂��H�v
����ςɕs�v�c�ł��B
�@�E�ƉȊw�҂����ɂƂ��ẮA�_���̐����҂����Ƃ��l���̖ړI�ɂȂ��Ă���̂�������܂���B�܂��A�i�r�G�X�g�[�N�X�������̌��E���w�E���Ă��A���ԓ��̒N��������ӂ���Ȃ��i�D����Ȃ��j���ƁA�Ƃ��ɓV�C�\��̂悤�ȁA���܂����𗧂�����p���嗬���߂錻�Ɓi�̐��j�E�ɂ����ẮA�u�i�r�G�X�g�[�N�X�������̂���������ȋߎ��̌��E�v���w�E����_���𓊍e���Ă��A�������Č����āA�_���f�ڂɑ�ςȍ�����������낤���Ƃ͎��ɂ͗e�Ղɑz���ł��܂��B
���{����
���W�[���X�J���F�k�S�����̐��w�I���_�i�Y�Ɛ}���A�P�X�V�X�j��
��҂��Ƃ����Ɏ��̕��͂����܂����B
�u�i����`�Ҕ����������́j���_�I�E��ʓI�A�����Ȑ��w��͓I�����́A���̖��̂��܂�̕��G���̂��߂ɁA�]�O�͂܂Ƃ܂����������Ȃ���Ȃ������Ƃ����̂��A���ۂ̂Ƃ���ł��邩������Ȃ��v
�u��₪�R�ς݂��Ă��邾���ɁA����̔��W�����҂����v
�u�Ō�ɁA3�����i�r�G�\�X�g�[�N�X�������̔�����̉��̑��I�E��ӓI���݂̖�肪�{���̏I�ǓI���̈�ł��邪�A���܂��ɖ������ł��邱�Ƃ́A�ȏ�̕����̌����ɑ���ő�̗��_�I��Q�ƂȂ邱�Ƃ𒍈ӂ��Ă������v
�Ə����Ă���܂����B
���������{�ŕ����w�������̂���߂Ă���1979�N�ɂ́A���łɓ��{�̏������w�̕���ł�
�u�i�r�G�X�g�[�N�X�������̍ő�̗��_�I��Q�v
���w�E����Ă����ɂ�������炸�A���͂��̃i�r�G�X�g�[�N�X�̓D���ɑ��ݓ���āA�������w�҂��w�E�����c�_�̍ݏ��Ɏ��͂悤�₭���ǂ�����̂�������܂���B
�@�Ƃ��Ƀ\�A�̏������w�҂̖{�́A�ǂ݂₷���͂Ȃ��̂ł����A���W�[���X�J���̖�{��6�y�[�W�̉�����7�s�ڂ�
�u�i�r�G�X�g�[�N�X���������A���v�͊w�̃}�b�N�X�E�G���[�{���c�}�����������瓱���ۂɗp�����ADmxV����r�I�������Ƃ��鉼��͖�������Ȃ��Ȃ邾�낤�v
�Ƃ����Ă��܂��B���W�[���X�J��������DmxV �Ƃ����̂������Ӗ�����̂��A���ɂ͂킩��܂��A�{���c�}����
�P�D�C�̂ŏՓ˂̏u�Ԃ������ݍ�p����
�Q�D���E�ł͑��ݍ�p�i�M�����A���������j�Ȃ�
�����肵�āA�C�̕��q�W�c�i���Ȃ킿���̗��q�j�̉^���ʕۑ������Ă��܂��B���������āA�u�{���c�}���̉���P�Ɖ���2���A���݂̗����̎�����ϑ��f�[�^�ɍ���Ȃ��v�Ǝ��͎咣�������̂ŁA���W�[���X�J���̖{�̏��_�ɏ�����Ă���DmxV����ςɋC�ɂȂ�܂��B
�@���W�[���X�J���̖�{�̏��_�Ɩ�҂��Ƃ�����Y�t�������܂����A
���{����N